Skip to contents

Beyond Cluster Counts: Dual-Anchor Elicitation for Weight Control

JoonHo Lee

2026-01-01

Source: vignettes/dual-anchor.Rmd
dual-anchor.Rmd

Overview

The previous vignettes focused on calibrating a Gamma hyperprior for α\alpha based on your expectations about the number of clusters KJK_J. This approach is intuitive: you specify how many groups you expect, and the DPprior package finds the corresponding prior on α\alpha.

However, as Vicentini & Jermyn (2025) have pointed out, matching KJK_J alone can lead to unintended prior behavior on the cluster weights. Specifically, a prior that produces the “right” expected number of clusters may simultaneously imply a high probability that a single cluster dominates the entire mixture.

This vignette introduces the dual-anchor framework, which allows you to control both:

  1. Anchor 1: The number of occupied clusters KJK_J (as before)
  2. Anchor 2: A weight-related quantity (e.g., w1w_1 or ρ\rho) that captures how mass is distributed across clusters

By the end of this vignette, you will understand:

  • Why K-only calibration can produce surprising weight behavior
  • Two key weight anchors: w1w_1 and ρ\rho (co-clustering probability)
  • How to use DPprior_dual() for dual-anchor elicitation
  • When and how to choose between different anchors and λ\lambda values

1. The Hidden Problem: Unintended Weight Priors

1.1 What K-Only Calibration Misses

Consider a researcher analyzing a multisite educational trial with 50 sites, expecting that treatment effects will cluster into approximately 5 distinct patterns. Using the K-only calibration approach from the Applied Guide, they obtain:

J <- 50
mu_K <- 5

fit_K <- DPprior_fit(J = J, mu_K = mu_K, confidence = "low")
#> Warning: HIGH DOMINANCE RISK: P(w1 > 0.5) = 56.3% exceeds 40%.
#>   This may indicate unintended prior behavior (RN-07).
#>   Consider using DPprior_dual() for weight-constrained elicitation.
#>   See ?DPprior_diagnostics for interpretation.
print(fit_K)
#> DPprior Prior Elicitation Result
#> ============================================= 
#> 
#> Gamma Hyperprior: α ~ Gamma(a = 0.5178, b = 0.3410)
#>   E[α] = 1.519, SD[α] = 2.110
#> 
#> Target (J = 50):
#>   E[K_J]   = 5.00
#>   Var(K_J) = 20.00
#>   (from confidence = 'low')
#> 
#> Achieved:
#>   E[K_J] = 5.000000, Var(K_J) = 20.000000
#>   Residual = 9.51e-09
#> 
#> Method: A2-MN (10 iterations)
#> 
#> Dominance Risk: HIGH ✘ (P(w₁>0.5) = 56%)

The fit looks reasonable: the prior expects about 5 clusters with appropriate uncertainty. But what does this prior imply about how mass is distributed across those clusters?

# Examine the implied weight behavior
cat("Weight diagnostics for K-only prior:\n")
#> Weight diagnostics for K-only prior:
cat("  E[w₁] =", round(mean_w1(fit_K$a, fit_K$b), 3), "\n")
#>   E[w₁] = 0.585
cat("  P(w₁ > 0.3) =", round(prob_w1_exceeds(0.3, fit_K$a, fit_K$b), 3), "\n")
#>   P(w₁ > 0.3) = 0.69
cat("  P(w₁ > 0.5) =", round(prob_w1_exceeds(0.5, fit_K$a, fit_K$b), 3), "\n")
#>   P(w₁ > 0.5) = 0.563
cat("  P(w₁ > 0.9) =", round(prob_w1_exceeds(0.9, fit_K$a, fit_K$b), 3), "\n")
#>   P(w₁ > 0.9) = 0.346

Here is the key insight: even though we expect only 5 clusters on average, there is a substantial probability (nearly 50%!) that a randomly selected unit belongs to a cluster containing more than half of all units. This is much more concentrated than many researchers would intuitively expect from “5 clusters.”

1.2 Why Does This Happen?

The relationship between KJK_J and the cluster weights is not as tight as one might expect. The expected number of clusters follows approximately:

𝔼[KJ∣α]≈1+αlogJ \mathbb{E}[K_J \mid \alpha] \approx 1 + \alpha \log J

while the expected first stick-breaking weight is:

𝔼[w1∣α]=11+α \mathbb{E}[w_1 \mid \alpha] = \frac{1}{1 + \alpha}

For J=50J = 50 and an expected cluster count around 5, we need α≈1\alpha \approx 1, which implies 𝔼[w1∣α]≈0.5\mathbb{E}[w_1 \mid \alpha] \approx 0.5. But because α\alpha is random under our Gamma hyperprior, the tails of the α\alpha distribution can induce extreme weight behavior: small α\alpha values lead to w1w_1 close to 1, while large α\alpha values fragment the weights.

# Illustrate the conditional relationship
alpha_grid <- c(0.5, 1, 2, 5, 10, 20)
w_grid <- seq(0.01, 0.99, length.out = 200)

cond_df <- do.call(rbind, lapply(alpha_grid, function(a) {
  data.frame(
    w = w_grid,
    density = dbeta(w_grid, 1, a),
    alpha = paste0("α = ", a)
  )
}))
cond_df$alpha <- factor(cond_df$alpha, levels = paste0("α = ", alpha_grid))

ggplot(cond_df, aes(x = w, y = density, color = alpha)) +
  geom_line(linewidth = 0.8) +
  scale_color_viridis_d(option = "plasma", end = 0.85) +
  labs(
    x = expression(w[1]),
    y = "Conditional Density",
    title = expression("Conditional Distribution of " * w[1] * " | " * alpha),
    color = NULL
  ) +
  theme_minimal() +
  theme(legend.position = "right")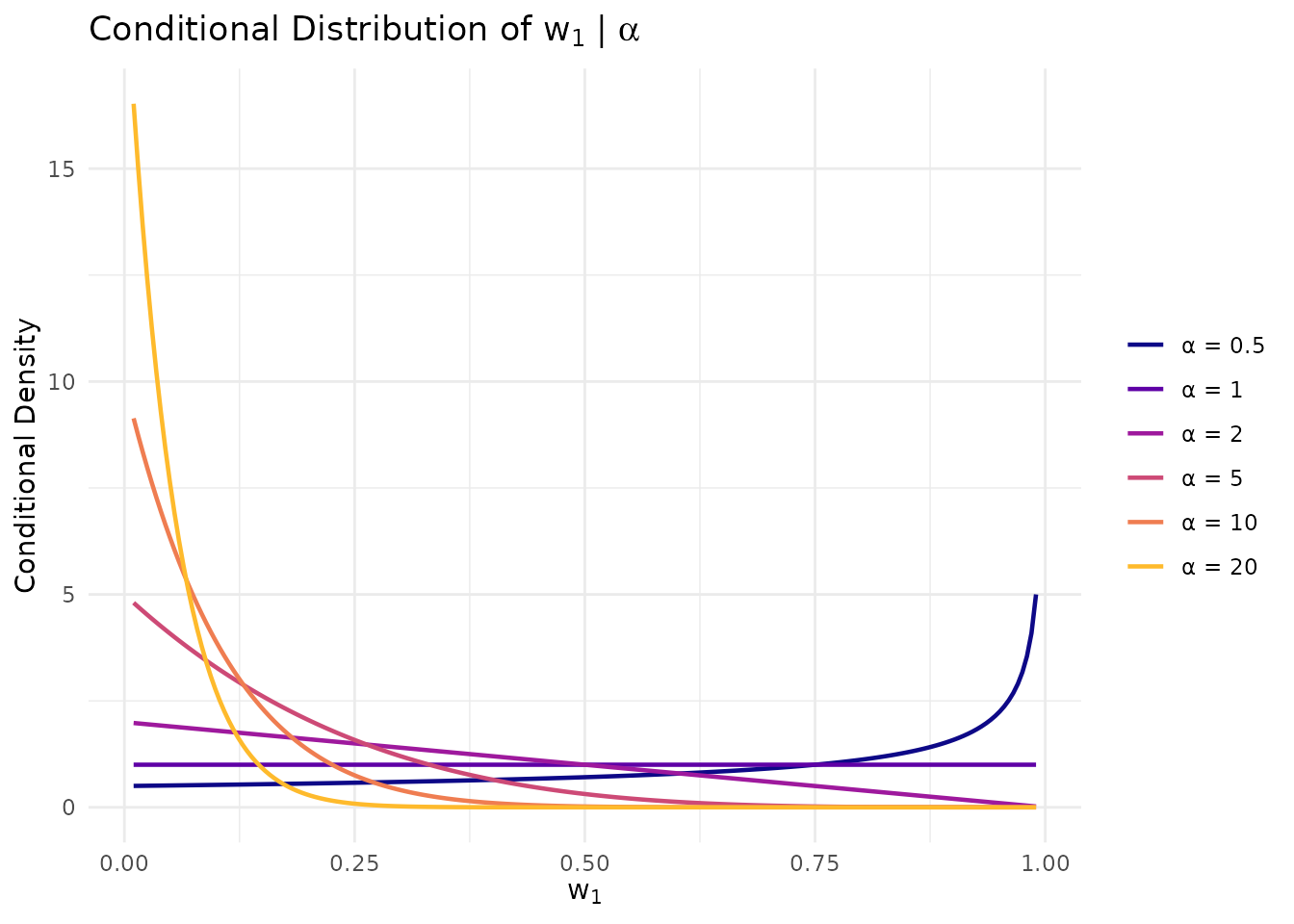
When α is small, w₁ concentrates near 1; when α is large, w₁ concentrates near 0. A diffuse prior on α spans both extremes.

When α is small, w₁ concentrates near 1; when α is large, w₁ concentrates near 0. A diffuse prior on α spans both extremes.

2. Understanding Weight Distributions

Before diving into dual-anchor calibration, let us examine the two weight anchors available in the DPprior package.

2.1 Stick-Breaking Weights Refresher

Under Sethuraman’s stick-breaking representation of the Dirichlet Process, the random mixing measure GG is:

G=∑h=1∞whδθh G = \sum_{h=1}^{\infty} w_h \, \delta_{\theta_h}

where the weights are constructed via:

vh∼iidBeta(1,α),w1=v1,wh=vh∏ℓ<h(1−vℓ)(h≥2) v_h \overset{iid}{\sim} \text{Beta}(1, \alpha), \quad w_1 = v_1, \quad w_h = v_h \prod_{\ell < h} (1 - v_\ell) \quad (h \geq 2)

The sequence (w1,w2,…)(w_1, w_2, \ldots) follows the GEM(α\alpha) distribution and is in size-biased order, not ranked by magnitude.

2.2 Anchor 2a: The First Stick-Breaking Weight (w1w_1)

The first weight w1w_1 has a particularly tractable distribution. Conditionally, w1∣α∼Beta(1,α)w_1 \mid \alpha \sim \text{Beta}(1, \alpha).

Under the hyperprior α∼Gamma(a,b)\alpha \sim \text{Gamma}(a, b), the marginal distribution of w1w_1 has fully closed-form expressions:

CDF: Fw1(x∣a,b)=1−(bb−log(1−x))a F_{w_1}(x \mid a, b) = 1 - \left( \frac{b}{b - \log(1-x)} \right)^a

Quantile function: Qw1(u∣a,b)=1−exp(b[1−(1−u)−1/a]) Q_{w_1}(u \mid a, b) = 1 - \exp\left( b \left[ 1 - (1-u)^{-1/a} \right] \right)

Survival function (dominance risk): P(w1>t∣a,b)=(bb−log(1−t))a P(w_1 > t \mid a, b) = \left( \frac{b}{b - \log(1-t)} \right)^a

Important interpretability caveat: w1w_1 is in GEM (size-biased) order, not the largest cluster weight. A faithful interpretation is:

“w1w_1 is the asymptotic proportion of the cluster containing a randomly selected unit.”

This is still a meaningful dominance diagnostic—if P(w1>0.5)P(w_1 > 0.5) is high, then a randomly selected unit is likely to belong to a cluster that contains more than half the population.

# Using the closed-form w1 functions
a <- fit_K$a
b <- fit_K$b

cat("w₁ distribution under K-only prior:\n")
#> w₁ distribution under K-only prior:
cat("  Mean:     ", round(mean_w1(a, b), 4), "\n")
#>   Mean:      0.5854
cat("  Variance: ", round(var_w1(a, b), 4), "\n")
#>   Variance:  0.1331
cat("  Median:   ", round(quantile_w1(0.5, a, b), 4), "\n")
#>   Median:    0.6169
cat("  90th %ile:", round(quantile_w1(0.9, a, b), 4), "\n")
#>   90th %ile: 1
cat("\nDominance risk:\n")
#> 
#> Dominance risk:
cat("  P(w₁ > 0.3):", round(prob_w1_exceeds(0.3, a, b), 4), "\n")
#>   P(w₁ > 0.3): 0.6903
cat("  P(w₁ > 0.5):", round(prob_w1_exceeds(0.5, a, b), 4), "\n")
#>   P(w₁ > 0.5): 0.563
cat("  P(w₁ > 0.9):", round(prob_w1_exceeds(0.9, a, b), 4), "\n")
#>   P(w₁ > 0.9): 0.3463

2.3 Anchor 2b: Co-Clustering Probability (ρ\rho)

The co-clustering probability is defined as:

ρ=∑h=1∞wh2 \rho = \sum_{h=1}^{\infty} w_h^2

This has a natural interpretation: ρ\rho equals the probability that two randomly selected units belong to the same cluster. This may be more intuitive for applied researchers to elicit.

The conditional moments are simple:

𝔼[ρ∣α]=11+α,Var(ρ∣α)=2α(1+α)2(2+α)(3+α) \mathbb{E}[\rho \mid \alpha] = \frac{1}{1 + \alpha}, \quad \text{Var}(\rho \mid \alpha) = \frac{2\alpha}{(1+\alpha)^2(2+\alpha)(3+\alpha)}

Note that 𝔼[ρ∣α]=𝔼[w1∣α]\mathbb{E}[\rho \mid \alpha] = \mathbb{E}[w_1 \mid \alpha], so their means are equal, but their full distributions differ.

# Using the rho (co-clustering) functions
cat("Co-clustering probability ρ under K-only prior:\n")
#> Co-clustering probability ρ under K-only prior:
cat("  E[ρ]:     ", round(mean_rho(a, b), 4), "\n")
#>   E[ρ]:      0.5854
cat("  Var(ρ):   ", round(var_rho(a, b), 6), "\n")
#>   Var(ρ):    0.107831
cat("  SD(ρ):    ", round(sqrt(var_rho(a, b)), 4), "\n")
#>   SD(ρ):     0.3284

# Compare with w1
cat("\nNote: E[w₁] = E[ρ] =", round(mean_w1(a, b), 4), "\n")
#> 
#> Note: E[w₁] = E[ρ] = 0.5854
cat("But: Var(w₁) =", round(var_w1(a, b), 4), "≠ Var(ρ) =", 
    round(var_rho(a, b), 6), "\n")
#> But: Var(w₁) = 0.1331 ≠ Var(ρ) = 0.107831

3. The Dual-Anchor Framework

3.1 The Core Idea

The dual-anchor framework finds Gamma hyperparameters (a,b)(a, b) that satisfy two types of constraints simultaneously:

  • Anchor 1: Match your beliefs about KJK_J (number of clusters)
  • Anchor 2: Match your beliefs about a weight quantity T∈{w1,ρ}T \in \{w_1, \rho\}

This is formalized as an optimization problem:

(a*,b*)=argmina>0,b>0[λ⋅LK(a,b)+(1−λ)⋅Lw(a,b)] (a^*, b^*) = \arg\min_{a > 0, b > 0} \left[ \lambda \cdot L_K(a, b) + (1 - \lambda) \cdot L_w(a, b) \right]

where LKL_K measures the discrepancy from the K target and LwL_w measures the discrepancy from the weight target.

3.2 The Role of λ\lambda

The parameter λ∈[0,1]\lambda \in [0, 1] controls the trade-off between the two anchors:

λ\lambda Value Interpretation
λ=1\lambda = 1 K-only calibration (ignores weight anchor)
λ=0\lambda = 0 Weight-only calibration (ignores K anchor)
0.5≤λ<10.5 \leq \lambda < 1 K remains primary, weight provides secondary control
0<λ<0.50 < \lambda < 0.5 Weight becomes primary (rare in practice)

In most applications, we recommend λ∈[0.5,0.9]\lambda \in [0.5, 0.9], keeping the cluster count as the primary anchor while using the weight constraint to avoid unintended dominance behavior.

3.3 Loss Types: Balancing the Two Anchors

A critical implementation detail is how to scale the two loss components. The DPprior_dual() function offers three loss_type options:

loss_type Description When to Use
"relative" Normalizes losses by their baseline values Default; good balance
"adaptive" Estimates scale factors from anchor extremes More aggressive weight control
"absolute" Raw squared errors (not recommended) Legacy; scale mismatch issues

Why does this matter? The K-anchor loss and weight-anchor loss are measured in different units. Without proper scaling, the optimizer may effectively ignore one of the anchors. The "adaptive" option is particularly useful when you want λ=0.5\lambda = 0.5 to produce a meaningful compromise between the two anchors.

4. Using DPprior_dual() for Dual-Anchor Elicitation

The DPprior_dual() function refines a K-calibrated prior to also satisfy weight constraints.

4.1 Basic Usage: Probability Constraint

Suppose you want to ensure that the probability of extreme dominance is limited. Specifically, you want P(w1>0.5)≤0.25P(w_1 > 0.5) \leq 0.25:

# Step 1: Start with K-only calibration
fit_K <- DPprior_fit(J = 50, mu_K = 5, confidence = "low")
#> Warning: HIGH DOMINANCE RISK: P(w1 > 0.5) = 56.3% exceeds 40%.
#>   This may indicate unintended prior behavior (RN-07).
#>   Consider using DPprior_dual() for weight-constrained elicitation.
#>   See ?DPprior_diagnostics for interpretation.

cat("K-only prior:\n")
#> K-only prior:
cat("  Gamma(", round(fit_K$a, 3), ",", round(fit_K$b, 3), ")\n")
#>   Gamma( 0.518 , 0.341 )
cat("  P(w₁ > 0.5) =", round(prob_w1_exceeds(0.5, fit_K$a, fit_K$b), 3), "\n\n")
#>   P(w₁ > 0.5) = 0.563

# Step 2: Apply dual-anchor constraint with adaptive loss
fit_dual <- DPprior_dual(
  fit = fit_K,
  w1_target = list(prob = list(threshold = 0.5, value = 0.25)),
  lambda = 0.7,
  loss_type = "adaptive",  # More aggressive weight control
  verbose = FALSE
)

cat("Dual-anchor prior (adaptive):\n")
#> Dual-anchor prior (adaptive):
cat("  Gamma(", round(fit_dual$a, 3), ",", round(fit_dual$b, 3), ")\n")
#>   Gamma( 1.403 , 0.626 )
cat("  P(w₁ > 0.5) =", round(prob_w1_exceeds(0.5, fit_dual$a, fit_dual$b), 3), "\n")
#>   P(w₁ > 0.5) = 0.351

Let us visualize the effect on both the KJK_J and w1w_1 distributions:

# Prepare data for visualization
logS <- compute_log_stirling(J)

# K distributions
k_grid <- 1:20
k_df <- data.frame(
  K = rep(k_grid, 2),
  probability = c(
    pmf_K_marginal(J, fit_K$a, fit_K$b, logS = logS)[k_grid],
    pmf_K_marginal(J, fit_dual$a, fit_dual$b, logS = logS)[k_grid]
  ),
  Prior = rep(c("K-only", "Dual-anchor"), each = length(k_grid))
)

# w1 distributions
w_grid <- seq(0.01, 0.95, length.out = 200)
w_df <- data.frame(
  w1 = rep(w_grid, 2),
  density = c(
    density_w1(w_grid, fit_K$a, fit_K$b),
    density_w1(w_grid, fit_dual$a, fit_dual$b)
  ),
  Prior = rep(c("K-only", "Dual-anchor"), each = length(w_grid))
)

# Create plots
p1 <- ggplot(k_df, aes(x = K, y = probability, color = Prior)) +
  geom_point(size = 1.5) +
  geom_line(linewidth = 0.8) +
  scale_color_manual(values = palette_2) +
  labs(x = "Number of Clusters (K)", y = "Probability",
       title = "Marginal PMF of K") +
  theme_minimal() +
  theme(legend.position = "bottom")

p2 <- ggplot(w_df, aes(x = w1, y = density, color = Prior)) +
  geom_line(linewidth = 1) +
  geom_vline(xintercept = 0.5, linetype = "dashed", color = "gray50") +
  scale_color_manual(values = palette_2) +
  labs(x = expression(w[1]), y = "Density",
       title = expression("Marginal Density of " * w[1])) +
  theme_minimal() +
  theme(legend.position = "bottom")

gridExtra::grid.arrange(p1, p2, ncol = 2)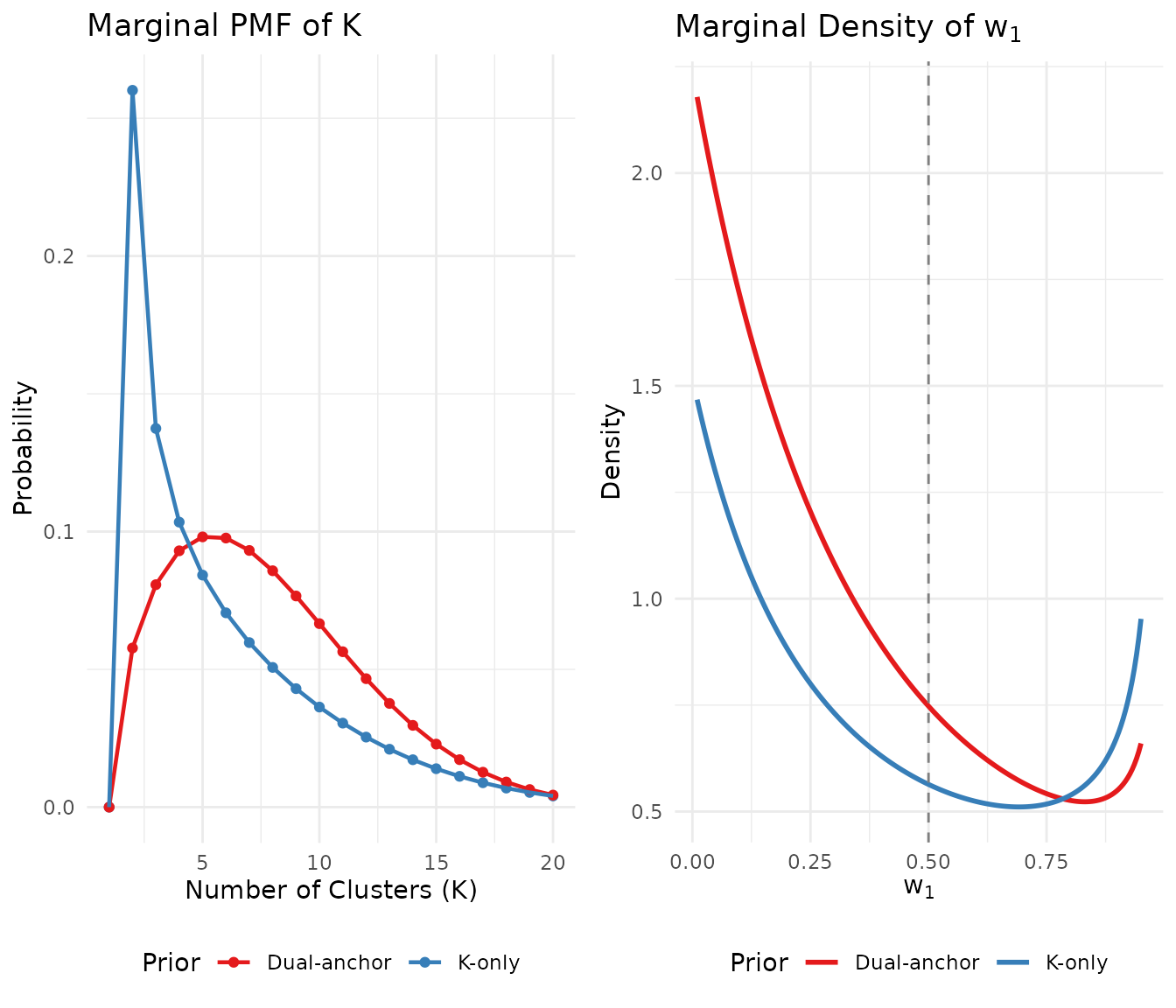
Comparison of K-only vs dual-anchor priors: the dual-anchor approach shifts mass away from extreme w₁ values while maintaining similar K expectations.

Comparison of K-only vs dual-anchor priors: the dual-anchor approach shifts mass away from extreme w₁ values while maintaining similar K expectations.

4.2 Comparing Loss Types

The choice of loss_type can significantly affect the results. Let us compare the three options:

# Compare loss types at lambda = 0.5
w1_target <- list(prob = list(threshold = 0.5, value = 0.25))

fit_relative <- DPprior_dual(
  fit_K, w1_target, lambda = 0.5, 
  loss_type = "relative", verbose = FALSE
)

fit_adaptive <- DPprior_dual(
  fit_K, w1_target, lambda = 0.5, 
  loss_type = "adaptive", verbose = FALSE
)

# Create comparison table
loss_compare <- data.frame(
  Method = c("K-only", "Relative", "Adaptive"),
  a = c(fit_K$a, fit_relative$a, fit_adaptive$a),
  b = c(fit_K$b, fit_relative$b, fit_adaptive$b),
  E_K = c(
    exact_K_moments(J, fit_K$a, fit_K$b)$mean,
    exact_K_moments(J, fit_relative$a, fit_relative$b)$mean,
    exact_K_moments(J, fit_adaptive$a, fit_adaptive$b)$mean
  ),
  P_w1_gt_50 = c(
    prob_w1_exceeds(0.5, fit_K$a, fit_K$b),
    prob_w1_exceeds(0.5, fit_relative$a, fit_relative$b),
    prob_w1_exceeds(0.5, fit_adaptive$a, fit_adaptive$b)
  )
)

loss_compare$a <- round(loss_compare$a, 3)
loss_compare$b <- round(loss_compare$b, 3)
loss_compare$E_K <- round(loss_compare$E_K, 2)
loss_compare$P_w1_gt_50 <- round(loss_compare$P_w1_gt_50, 3)

knitr::kable(
  loss_compare,
  col.names = c("Method", "a", "b", "E[K]", "P(w₁>0.5)"),
  caption = "Comparison of loss types at λ = 0.5 (target: P(w₁>0.5) = 0.25)"
)
Comparison of loss types at λ = 0.5 (target: P(w₁>0.5) = 0.25)
Method a b E[K] P(w₁>0.5)
K-only 0.518 0.341 5.00 0.563
Relative 0.736 0.424 5.63 0.490
Adaptive 1.737 0.715 7.43 0.308

The "adaptive" loss type typically produces more noticeable weight reduction because it normalizes each loss component by its scale at the opposite anchor’s optimum.

4.3 Alternative: Quantile Constraint

You can also specify a quantile constraint. For example, to ensure that the 90th percentile of w1w_1 does not exceed 0.6:

fit_dual_q <- DPprior_dual(
  fit = fit_K,
  w1_target = list(quantile = list(prob = 0.9, value = 0.6)),
  lambda = 0.7,
  loss_type = "adaptive",
  verbose = FALSE
)

cat("Dual-anchor (quantile constraint):\n")
#> Dual-anchor (quantile constraint):
cat("  Gamma(", round(fit_dual_q$a, 3), ",", round(fit_dual_q$b, 3), ")\n")
#>   Gamma( 0.518 , 0.341 )
cat("  90th percentile of w₁:", round(quantile_w1(0.9, fit_dual_q$a, fit_dual_q$b), 3), "\n")
#>   90th percentile of w₁: 1
cat("  (Target was 0.6)\n")
#>   (Target was 0.6)

4.4 Alternative: Mean Constraint

For constraints based on 𝔼[w1]\mathbb{E}[w_1]:

fit_dual_m <- DPprior_dual(
  fit = fit_K,
  w1_target = list(mean = 0.35),
  lambda = 0.6,
  loss_type = "adaptive",
  verbose = FALSE
)

cat("Dual-anchor (mean constraint):\n")
#> Dual-anchor (mean constraint):
cat("  Gamma(", round(fit_dual_m$a, 3), ",", round(fit_dual_m$b, 3), ")\n")
#>   Gamma( 1.377 , 0.621 )
cat("  E[w₁]:", round(mean_w1(fit_dual_m$a, fit_dual_m$b), 3), "\n")
#>   E[w₁]: 0.411
cat("  (Target was 0.35)\n")
#>   (Target was 0.35)

5. Elicitation Questions for Weight Anchors

Translating substantive knowledge into weight constraints requires careful framing. Here are suggested elicitation questions:

For w1w_1 (Size-Biased Weight)

These questions focus on what happens when you randomly sample a unit:

“If you randomly select a site from your study, what proportion of all sites would you expect to share its effect pattern? What’s a reasonable median estimate?”

“Is there a significant chance (say, > 30%) that a randomly selected site belongs to an effect group that contains more than half of all sites?”

For ρ\rho (Co-Clustering Probability)

These questions may be more intuitive for many researchers:

“If you pick two sites at random, what’s the probability that they belong to the same effect group?”

“How likely is it that any two randomly chosen sites would show substantively similar treatment effects?”

Translation Examples

Elicited Belief Formal Constraint
“Randomly selected site’s group is ~25% of total (median)” quantile = list(prob = 0.5, value = 0.25)
“Unlikely (≤20%) that random site is in a dominant (>50%) group” prob = list(threshold = 0.5, value = 0.2)
“Two random sites have ~20% chance of same group” Use ρ\rho anchor with target mean 0.2

6. Exploring the Trade-off: λ\lambda Sensitivity

Different values of λ\lambda produce different trade-offs between matching the K anchor and the weight anchor. Let us explore this systematically:

lambda_grid <- c(1.0, 0.9, 0.7, 0.5, 0.3)
w1_target <- list(prob = list(threshold = 0.5, value = 0.2))

lambda_results <- lapply(lambda_grid, function(lam) {
  if (lam == 1.0) {
    # lambda = 1 just returns K-only
    fit <- fit_K
    fit$dual_anchor <- list(lambda = 1.0)
  } else {
    fit <- DPprior_dual(fit_K, w1_target, lambda = lam, 
                        loss_type = "adaptive", verbose = FALSE)
  }
  
  list(
    lambda = lam,
    a = fit$a,
    b = fit$b,
    E_K = exact_K_moments(J, fit$a, fit$b)$mean,
    P_w1_gt_50 = prob_w1_exceeds(0.5, fit$a, fit$b),
    E_w1 = mean_w1(fit$a, fit$b)
  )
})

# Create comparison table
lambda_df <- do.call(rbind, lapply(lambda_results, function(r) {
  data.frame(
    lambda = r$lambda,
    a = round(r$a, 3),
    b = round(r$b, 3),
    E_K = round(r$E_K, 2),
    P_w1_gt_50 = round(r$P_w1_gt_50, 3),
    E_w1 = round(r$E_w1, 3)
  )
}))

knitr::kable(
  lambda_df,
  col.names = c("λ", "a", "b", "E[K]", "P(w₁>0.5)", "E[w₁]"),
  caption = "Effect of λ on dual-anchor calibration (target: P(w₁>0.5) = 0.2, adaptive loss)"
)
Effect of λ on dual-anchor calibration (target: P(w₁>0.5) = 0.2, adaptive loss)
λ a b E[K] P(w₁>0.5) E[w₁]
1.0 0.518 0.341 5.00 0.563 0.585
0.9 1.032 0.520 6.31 0.417 0.460
0.7 1.658 0.694 7.33 0.317 0.381
0.5 2.143 0.819 7.87 0.269 0.344
0.3 2.597 0.933 8.26 0.236 0.320 
# Visualize the trade-off
tradeoff_df <- data.frame(
  lambda = sapply(lambda_results, `[[`, "lambda"),
  E_K = sapply(lambda_results, `[[`, "E_K"),
  P_w1 = sapply(lambda_results, `[[`, "P_w1_gt_50")
)

ggplot(tradeoff_df, aes(x = E_K, y = P_w1)) +
  geom_path(color = "gray50", linewidth = 0.8) +
  geom_point(aes(color = factor(lambda)), size = 4) +
  geom_hline(yintercept = 0.2, linetype = "dashed", color = "#E41A1C", alpha = 0.7) +
  geom_vline(xintercept = 5, linetype = "dashed", color = "#377EB8", alpha = 0.7) +
  annotate("text", x = 4.7, y = 0.22, label = "w₁ target", hjust = 1, color = "#E41A1C") +
  annotate("text", x = 5.1, y = 0.45, label = "K target", hjust = 0, color = "#377EB8") +
  scale_color_viridis_d(option = "viridis", begin = 0.2, end = 0.8) +
  labs(
    x = "E[K] (Cluster Count)",
    y = expression(P(w[1] > 0.5)),
    title = "Trade-off Between K and Weight Anchors",
    color = "λ"
  ) +
  theme_minimal() +
  theme(legend.position = "right")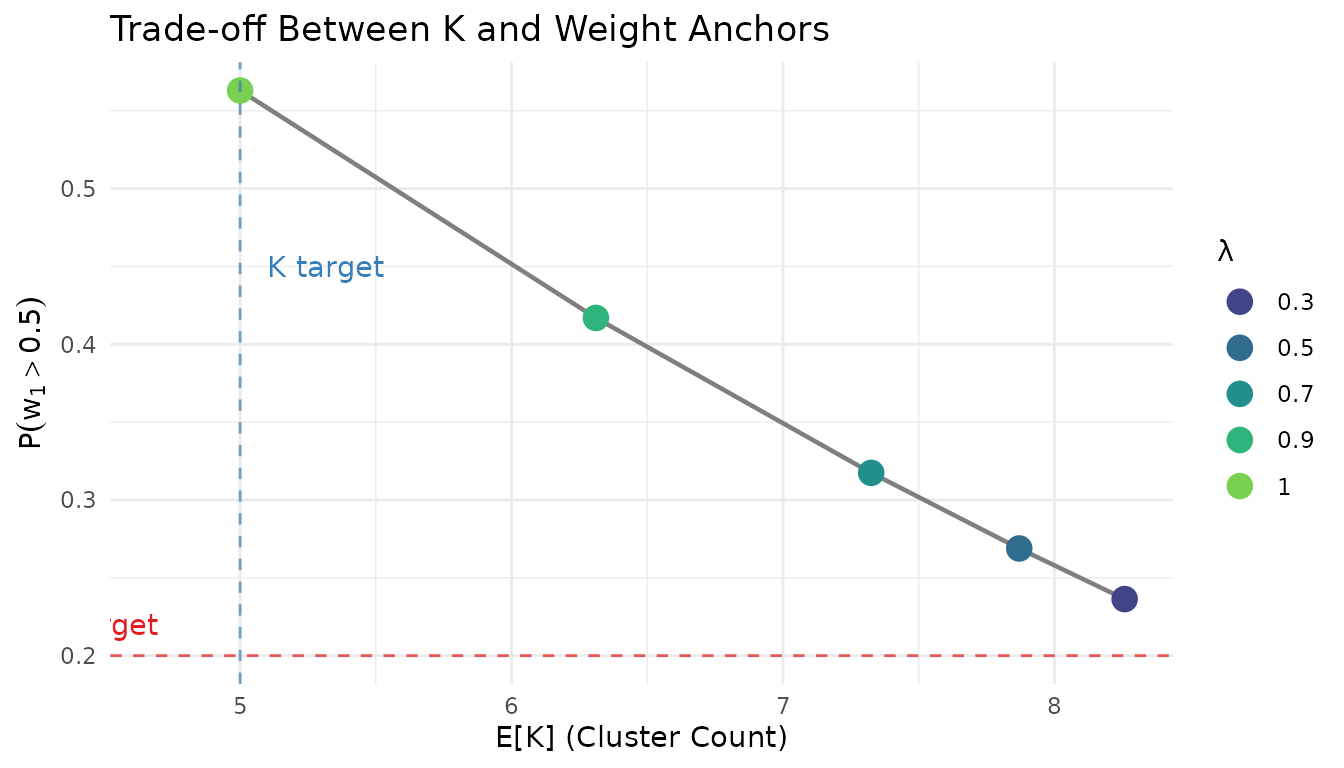
Trade-off curve: reducing λ brings P(w₁ > 0.5) closer to target at the cost of K deviation.

Trade-off curve: reducing λ brings P(w₁ > 0.5) closer to target at the cost of K deviation.

7. Practical Recommendations

7.1 When to Use Dual-Anchor Calibration

Consider dual-anchor calibration when:

  • High dominance risk in K-only fit: If print(fit) shows “Dominance Risk: HIGH” or P(w1>0.5)>0.4P(w_1 > 0.5) > 0.4

  • Strong prior belief against concentration: You believe effects should be reasonably spread across groups, not concentrated

  • Low-information settings: When the data may not strongly update the prior, unintended weight behavior can persist to the posterior

Do not use dual-anchor when:

  • You are comfortable with the weight implications of your K-only prior
  • You have strong data that will overwhelm any prior specification
  • The additional complexity is not justified for your application

7.2 Choosing loss_type

loss_type When to Use
"relative" Default choice; balanced trade-off
"adaptive" When you want λ=0.5\lambda = 0.5 to give meaningful weight reduction
"absolute" Not recommended (legacy)

We generally recommend "adaptive" for most dual-anchor applications, as it ensures that both anchors contribute meaningfully to the optimization.

7.3 Choosing λ\lambda

Situation Recommended λ\lambda
K anchor is well-justified, weight is secondary constraint 0.8 – 0.9
Both anchors are equally important 0.5 – 0.7
Weight behavior is primary concern 0.3 – 0.5

In practice, we recommend starting with λ=0.7\lambda = 0.7 and adjusting based on how closely each target is achieved.

7.4 Choosing Between w1w_1 and ρ\rho

Anchor Advantages Best For
w1w_1 Closed-form CDF/quantiles; dominance-focused Constraining tail behavior
ρ\rho More intuitive interpretation; moment-closed Mean-based elicitation

Since 𝔼[w1]=𝔼[ρ]\mathbb{E}[w_1] = \mathbb{E}[\rho], mean-based constraints are equivalent between the two anchors.

8. When Dual-Anchor Constraints Are Infeasible

Not all combinations of K and weight targets are achievable. If you specify conflicting constraints, the optimization may not fully satisfy both:

# An aggressive weight target that conflicts with K target
fit_aggressive <- DPprior_dual(
  fit = fit_K,
  w1_target = list(prob = list(threshold = 0.5, value = 0.05)),  # Very tight
  lambda = 0.5,
  loss_type = "adaptive",
  verbose = FALSE
)

cat("Aggressive dual-anchor attempt:\n")
#> Aggressive dual-anchor attempt:
cat("  Target: P(w₁ > 0.5) = 0.05\n")
#>   Target: P(w₁ > 0.5) = 0.05
cat("  Achieved: P(w₁ > 0.5) =", 
    round(prob_w1_exceeds(0.5, fit_aggressive$a, fit_aggressive$b), 3), "\n")
#>   Achieved: P(w₁ > 0.5) = 0.149
cat("\n  Target: E[K] = 5\n")
#> 
#>   Target: E[K] = 5
cat("  Achieved: E[K] =", 
    round(exact_K_moments(J, fit_aggressive$a, fit_aggressive$b)$mean, 2), "\n")
#>   Achieved: E[K] = 9.41

When constraints are too strict, consider:

  1. Relaxing one of the targets: Accept somewhat higher dominance risk or a different K expectation

  2. Adjusting λ\lambda: If one target is more important, weight it more heavily

  3. Using a single anchor: Sometimes K-only or weight-only calibration is more appropriate

Summary

Concept Key Point
K-only calibration May induce unintended weight behavior
w1w_1 (first weight) Size-biased cluster mass; closed-form distribution
ρ\rho (co-clustering) P(two random units share a cluster); intuitive
loss_type Use "adaptive" for meaningful trade-offs
Dual-anchor objective Trade-off between K fit and weight fit via λ\lambda
Recommended workflow 1. K-only fit → 2. Check diagnostics → 3. Dual-anchor if needed

What’s Next?

References

Vicentini, S., & Jermyn, I. H. (2025). Prior selection for the precision parameter of Dirichlet process mixture models. arXiv:2502.00864. https://doi.org/10.48550/arXiv.2502.00864

Sethuraman, J. (1994). A constructive definition of Dirichlet priors. Statistica Sinica, 4(2), 639–650.

For questions or feedback, please visit the GitHub repository.