Case Studies: Multisite Trials and Meta-Analysis

Overview

This vignette presents three case studies demonstrating how to apply the DPprior package in real-world research contexts. Each case study walks through the complete workflow—from substantive considerations to final prior specification—using published research as a foundation.

The three case studies span different domains and data structures:

Case Study	Domain	J (Sites/Studies)	Key Characteristic
1. Conditional Cash Transfer Trial	Education/Policy	38	Moderate sites, dual-anchor refinement
2. Brief Alcohol Interventions	Public Health	117	Large meta-analysis, multiple heterogeneity sources
3. Alabama Pre-K Value-Added	Education Policy	500 (of 847)	Large-scale policy evaluation

By working through these examples, you will learn how to:

Translate substantive domain knowledge into cluster count expectations
Choose appropriate calibration methods for different settings
Apply diagnostics to verify prior behavior
Conduct sensitivity analysis across specifications
Report prior elicitation transparently in publications

1. Case Study: Conditional Cash Transfer Multisite Trial

1.1 Research Context

Our first case study draws from the multisite conditional cash transfer (CCT) experiment analyzed in Lee et al. (2025). The Conditional Subsidies for School Attendance program, implemented in Bogotá, Colombia (Barrera-Osorio et al., 2019), conducted randomized experiments across 38 sites in the San Cristobal district.

Study characteristics:

Sample size: 6,506 participants nested within 38 sites
Average site size: 171.2 participants
Coefficient of variation in site sizes: 0.67 (range: 23 to 484)
Outcomes: Secondary school enrollment and on-time graduation
Key feature: Large within-site information, limited between-site variation

1.2 The Inferential Goals

The researchers sought to understand the distribution of site-specific treatment effects $\tau_j$ , with particular interest in:

Estimating the variance of the prior distribution $G$
Identifying extreme sites (10th and 90th percentiles)
Understanding heterogeneity patterns across sites

Given the estimated cross-site effect standard deviation of $\sigma = 0.04$ to $0.06$ (in effect size units) and relatively high within-site precision, this setting exhibits small between-site information and large within-site information—a configuration where prior choice substantially influences posterior inference.

1.3 Initial Prior Elicitation

Step 1: Determining the expected number of clusters

When eliciting prior beliefs about cluster structure, researchers might consider several substantive factors:

The intervention was implemented uniformly across sites, suggesting limited structural heterogeneity
However, local context (school culture, neighborhood characteristics) might create differential responses
Previous multisite education trials typically exhibit 3–8 distinct response patterns

Based on these considerations, a reasonable expectation is approximately $\mu_K = 5$ clusters among the 38 sites.

# Define the study context
J_cct <- 38
mu_K_cct <- 5

cat("Study context:\n")
#> Study context:
cat("  Number of sites (J):", J_cct, "\n")
#>   Number of sites (J): 38
cat("  Expected clusters (μ_K):", mu_K_cct, "\n")
#>   Expected clusters (μ_K): 5
cat("  Ratio (μ_K/J):", round(mu_K_cct / J_cct, 3), "\n")
#>   Ratio (μ_K/J): 0.132

Step 2: Expressing uncertainty

Given the novelty of this specific intervention context and the moderate sample of sites, we should express substantial uncertainty. A “low” confidence level is appropriate:

# Initial fit with low confidence
fit_cct <- DPprior_fit(
  J = J_cct, 
  mu_K = mu_K_cct, 
  confidence = "low"
)
#> Warning: HIGH DOMINANCE RISK: P(w1 > 0.5) = 54.5% exceeds 40%.
#>   This may indicate unintended prior behavior (RN-07).
#>   Consider using DPprior_dual() for weight-constrained elicitation.
#>   See ?DPprior_diagnostics for interpretation.

print(fit_cct)
#> DPprior Prior Elicitation Result
#> ============================================= 
#> 
#> Gamma Hyperprior: α ~ Gamma(a = 0.4629, b = 0.2556)
#>   E[α] = 1.811, SD[α] = 2.662
#> 
#> Target (J = 38):
#>   E[K_J]   = 5.00
#>   Var(K_J) = 20.00
#>   (from confidence = 'low')
#> 
#> Achieved:
#>   E[K_J] = 5.000000, Var(K_J) = 20.000000
#>   Residual = 6.09e-09
#> 
#> Method: A2-MN (11 iterations)
#> 
#> Dominance Risk: HIGH ✘ (P(w₁>0.5) = 54%)

1.4 Comprehensive Diagnostics

Before accepting this prior, we need to verify its behavior across multiple dimensions. The DPprior_diagnostics() function provides a comprehensive assessment:

diag_cct <- DPprior_diagnostics(fit_cct)

cat("=== Comprehensive Diagnostic Report ===\n\n")
#> === Comprehensive Diagnostic Report ===

cat("1. ALPHA DISTRIBUTION\n")
#> 1. ALPHA DISTRIBUTION
cat("   Mean:     ", round(diag_cct$alpha$mean, 3), "\n")
#>    Mean:      1.811
cat("   SD:       ", round(diag_cct$alpha$sd, 3), "\n")
#>    SD:        2.662
cat("   CV:       ", round(diag_cct$alpha$cv, 3), "\n")
#>    CV:        1.47
cat("   5th %ile: ", round(diag_cct$alpha$quantiles["q5"], 3), "\n")
#>    5th %ile:  0.005
cat("   50th %ile:", round(diag_cct$alpha$quantiles["q50"], 3), "\n")
#>    50th %ile: 0.767
cat("   95th %ile:", round(diag_cct$alpha$quantiles["q95"], 3), "\n")
#>    95th %ile: 7.15

cat("\n2. CLUSTER COUNT (K)\n")
#> 
#> 2. CLUSTER COUNT (K)
cat("   E[K]:     ", round(diag_cct$K$mean, 3), "\n")
#>    E[K]:      5
cat("   Var(K):   ", round(diag_cct$K$var, 3), "\n")
#>    Var(K):    20
cat("   SD(K):    ", round(sqrt(diag_cct$K$var), 3), "\n")
#>    SD(K):     4.472
cat("   Mode(K):  ", diag_cct$K$mode, "\n")
#>    Mode(K):   1

cat("\n3. WEIGHT BEHAVIOR\n")
#> 
#> 3. WEIGHT BEHAVIOR
cat("   E[w₁]:        ", round(diag_cct$weights$mean, 3), "\n")
#>    E[w₁]:         0.572
cat("   Median(w₁):   ", round(diag_cct$weights$median, 3), "\n")
#>    Median(w₁):    0.588
cat("   P(w₁ > 0.3):  ", round(diag_cct$weights$prob_exceeds["prob_gt_0.3"], 3), "\n")
#>    P(w₁ > 0.3):   NA
cat("   P(w₁ > 0.5):  ", round(diag_cct$weights$prob_exceeds["prob_gt_0.5"], 3), "\n")
#>    P(w₁ > 0.5):   0.545
cat("   P(w₁ > 0.9):  ", round(diag_cct$weights$prob_exceeds["prob_gt_0.9"], 3), "\n")
#>    P(w₁ > 0.9):   0.344
cat("   Dominance:    ", toupper(diag_cct$weights$dominance_risk), "\n")
#>    Dominance:     HIGH

cat("\n4. CO-CLUSTERING PROBABILITY (ρ)\n")
#> 
#> 4. CO-CLUSTERING PROBABILITY (ρ)
cat("   E[ρ]:         ", round(diag_cct$coclustering$mean, 3), "\n")
#>    E[ρ]:          0.572
cat("   Interpretation: Two random sites have a", 
    round(100 * diag_cct$coclustering$mean), "% chance of sharing a cluster\n")
#>    Interpretation: Two random sites have a 57 % chance of sharing a cluster

1.5 Visualizing the Initial Prior

The DPprior package provides several visualization functions to help understand prior behavior. Let’s examine each component:

Alpha distribution:

plot_alpha_prior(fit_cct)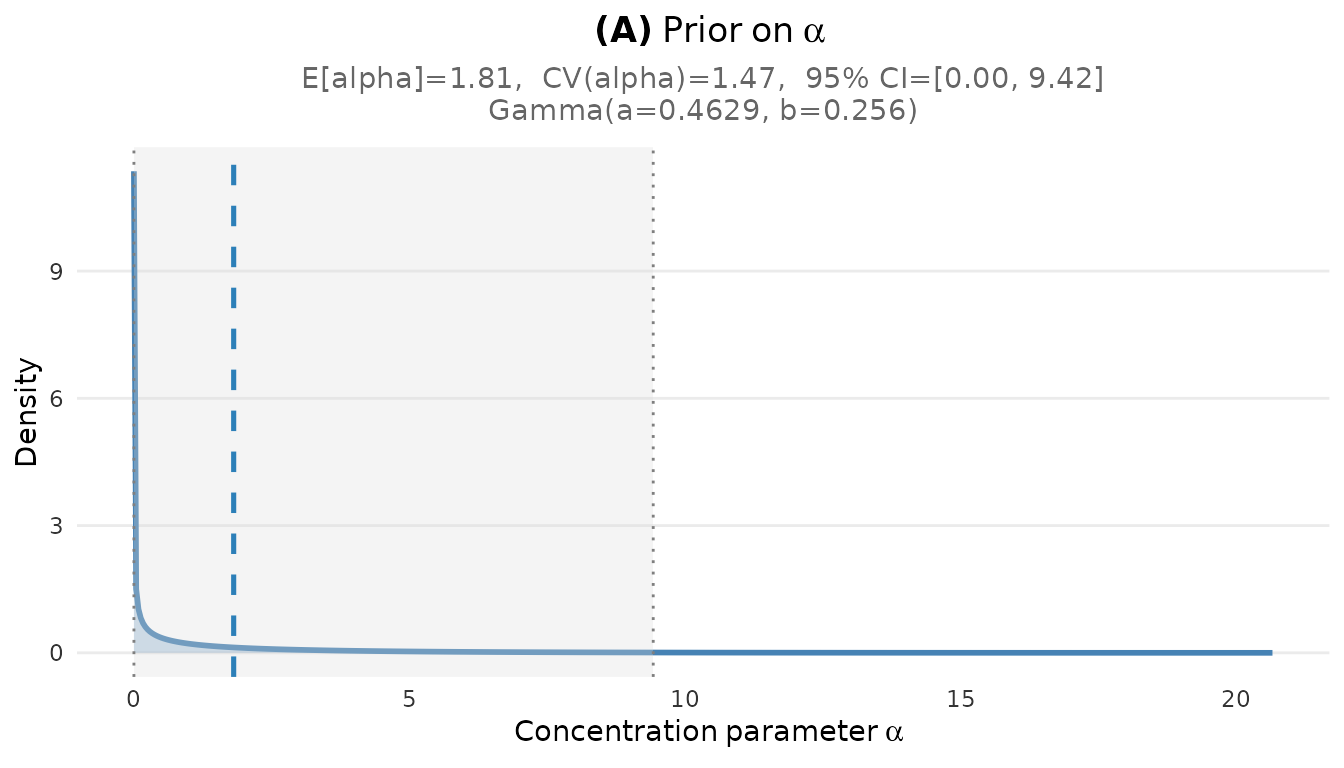

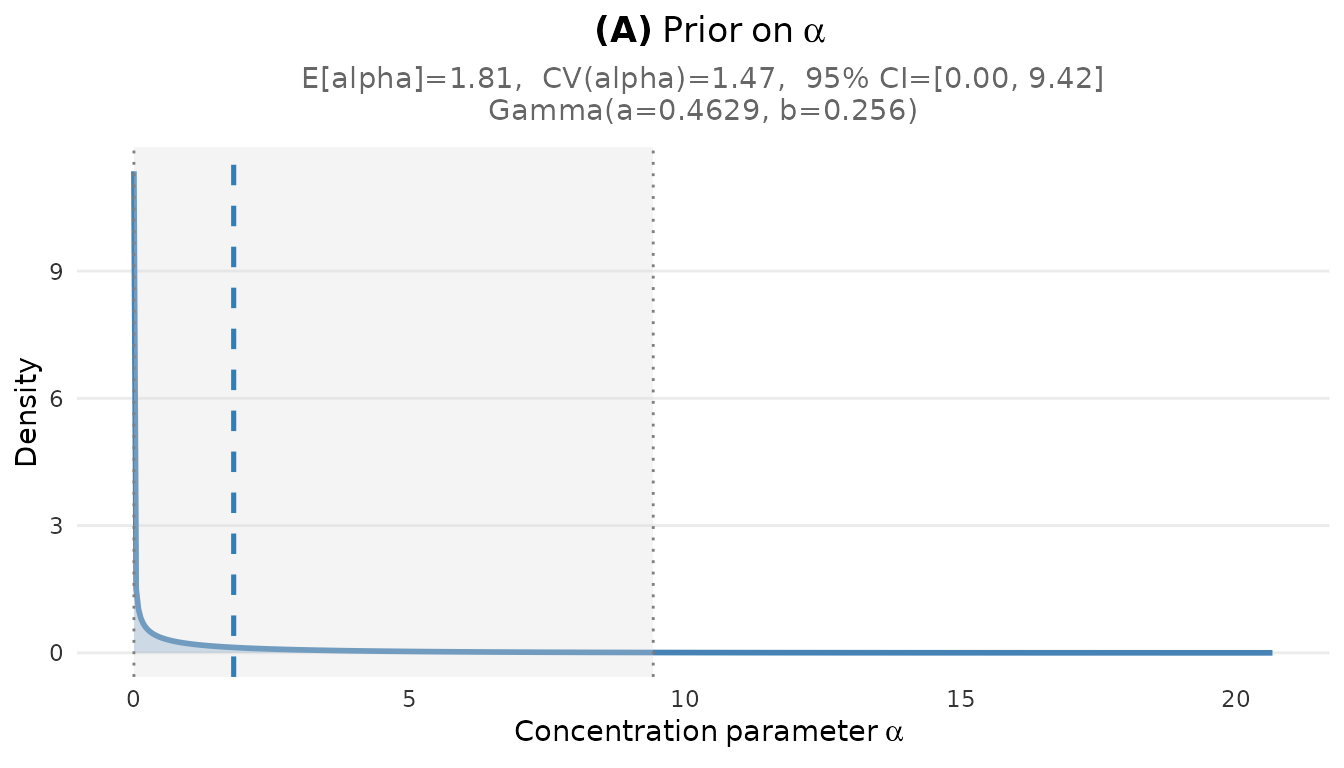
Prior distribution on the concentration parameter α for the CCT study.

Cluster count distribution:

plot_K_prior(fit_cct)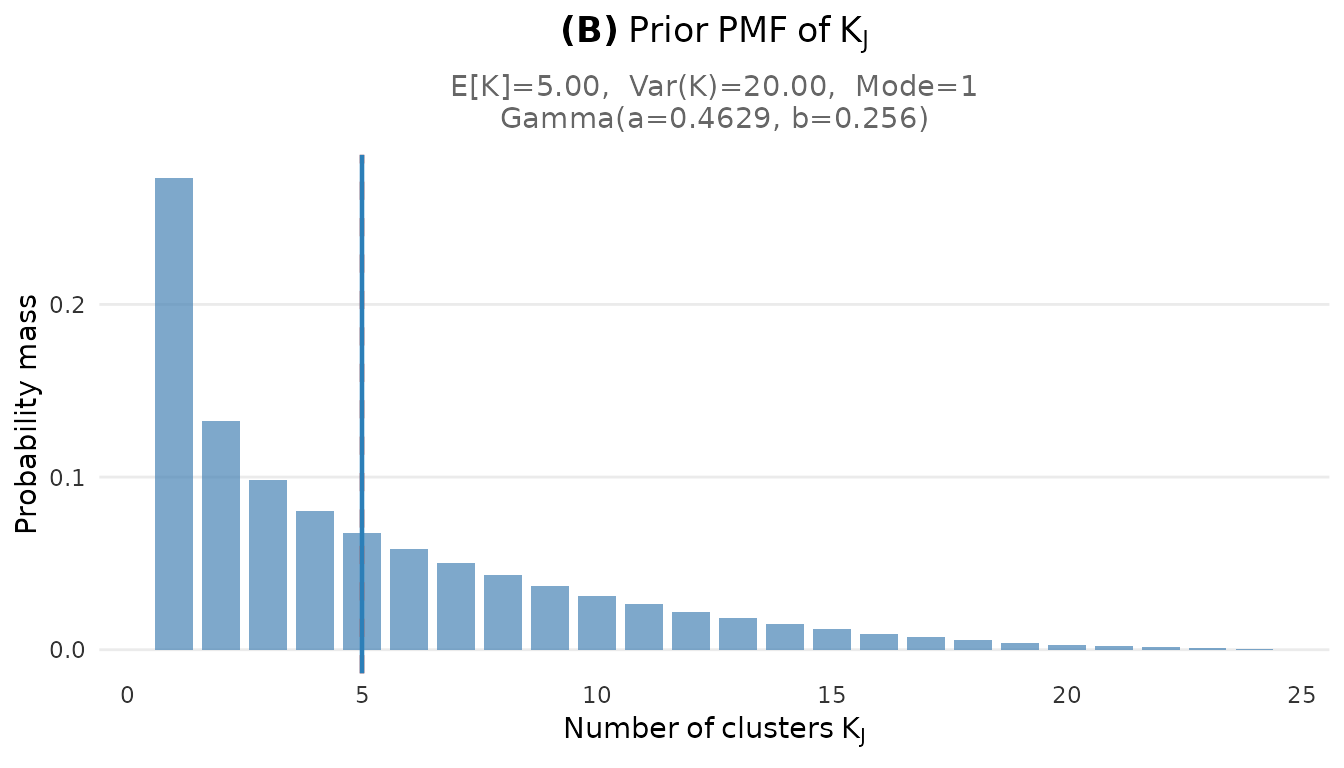

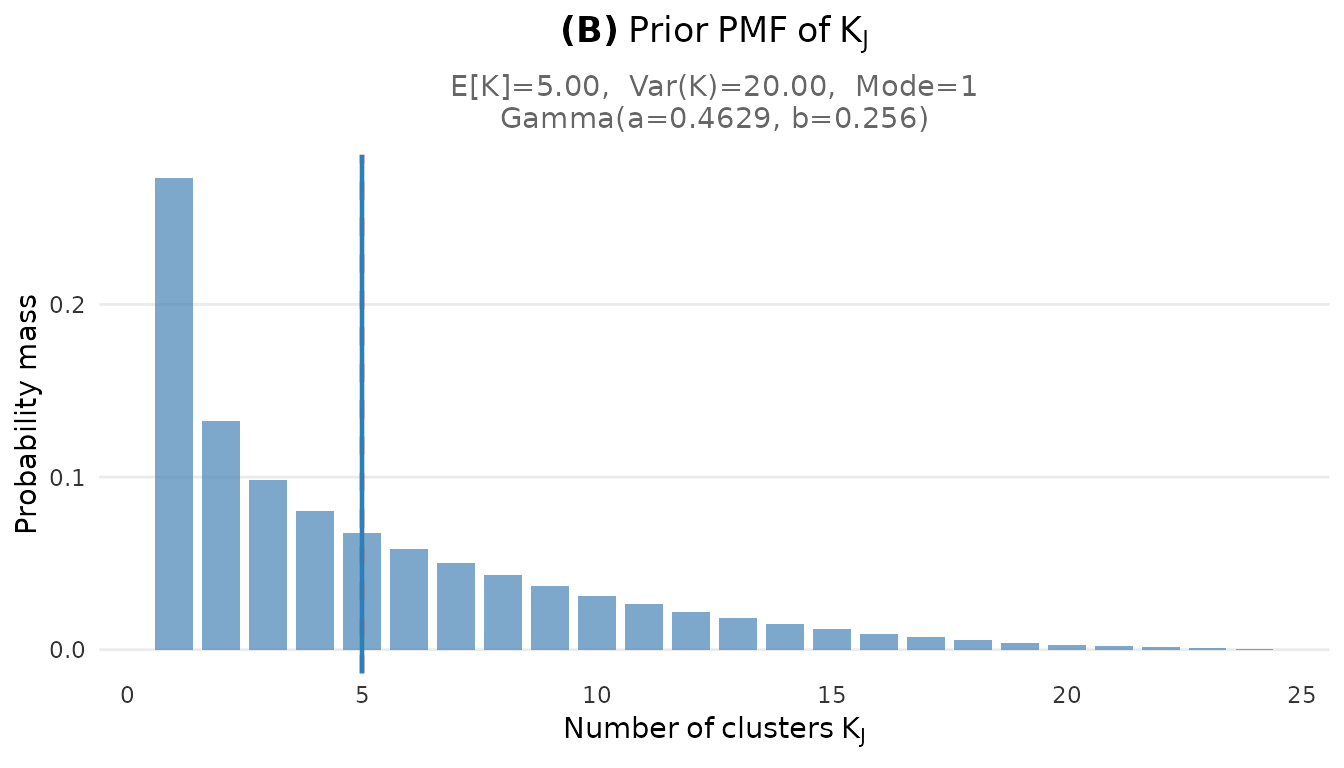
Prior PMF of the number of clusters K for the CCT study (J = 38).

Largest cluster weight distribution:

plot_w1_prior(fit_cct)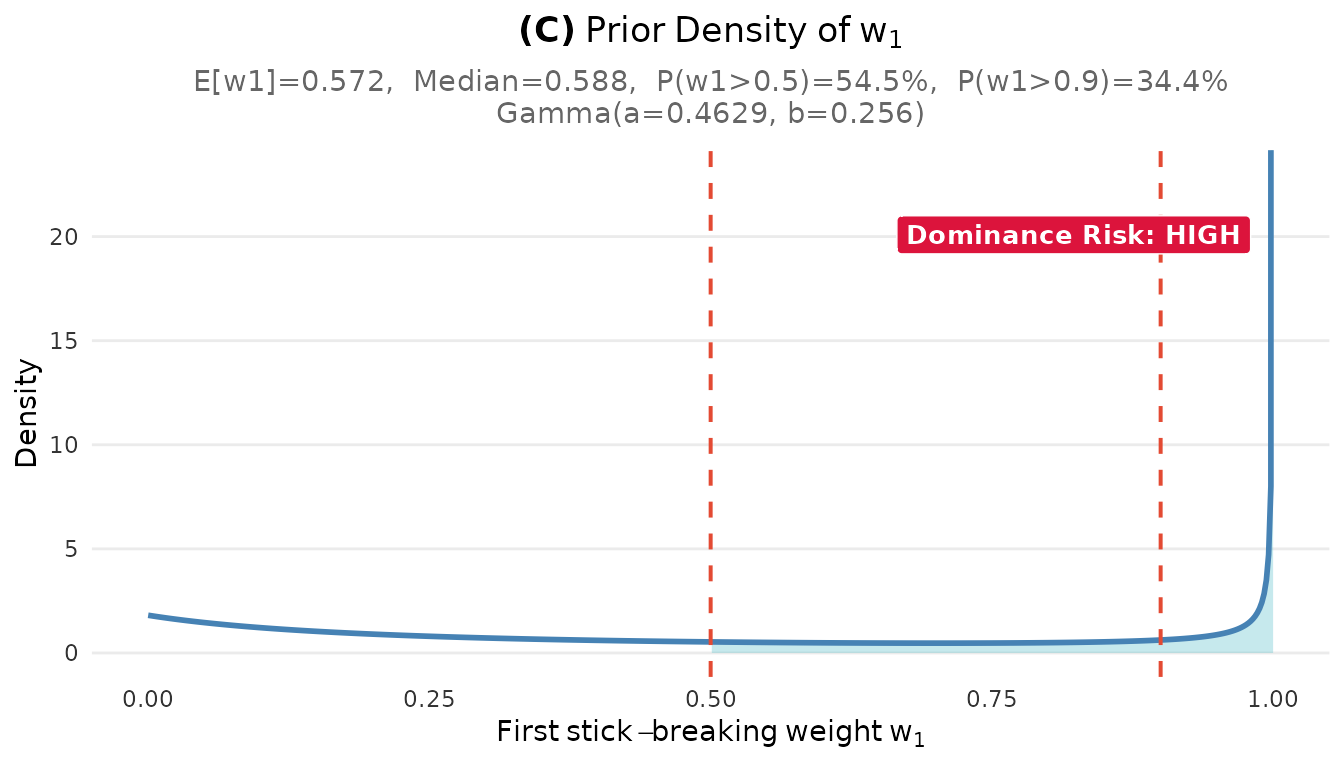

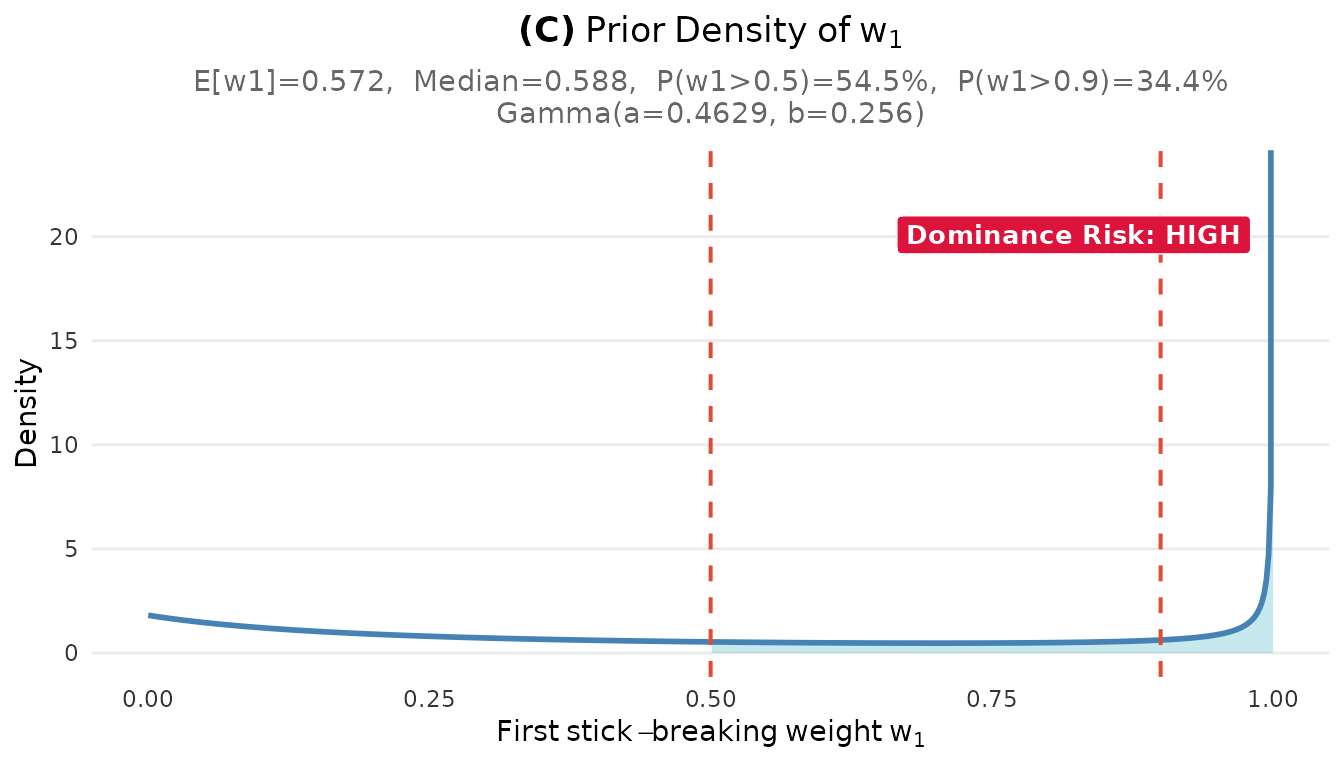
Prior distribution on the largest cluster weight w₁. The dashed line at 0.5 indicates the dominance threshold.

Complete dashboard:

plot(fit_cct)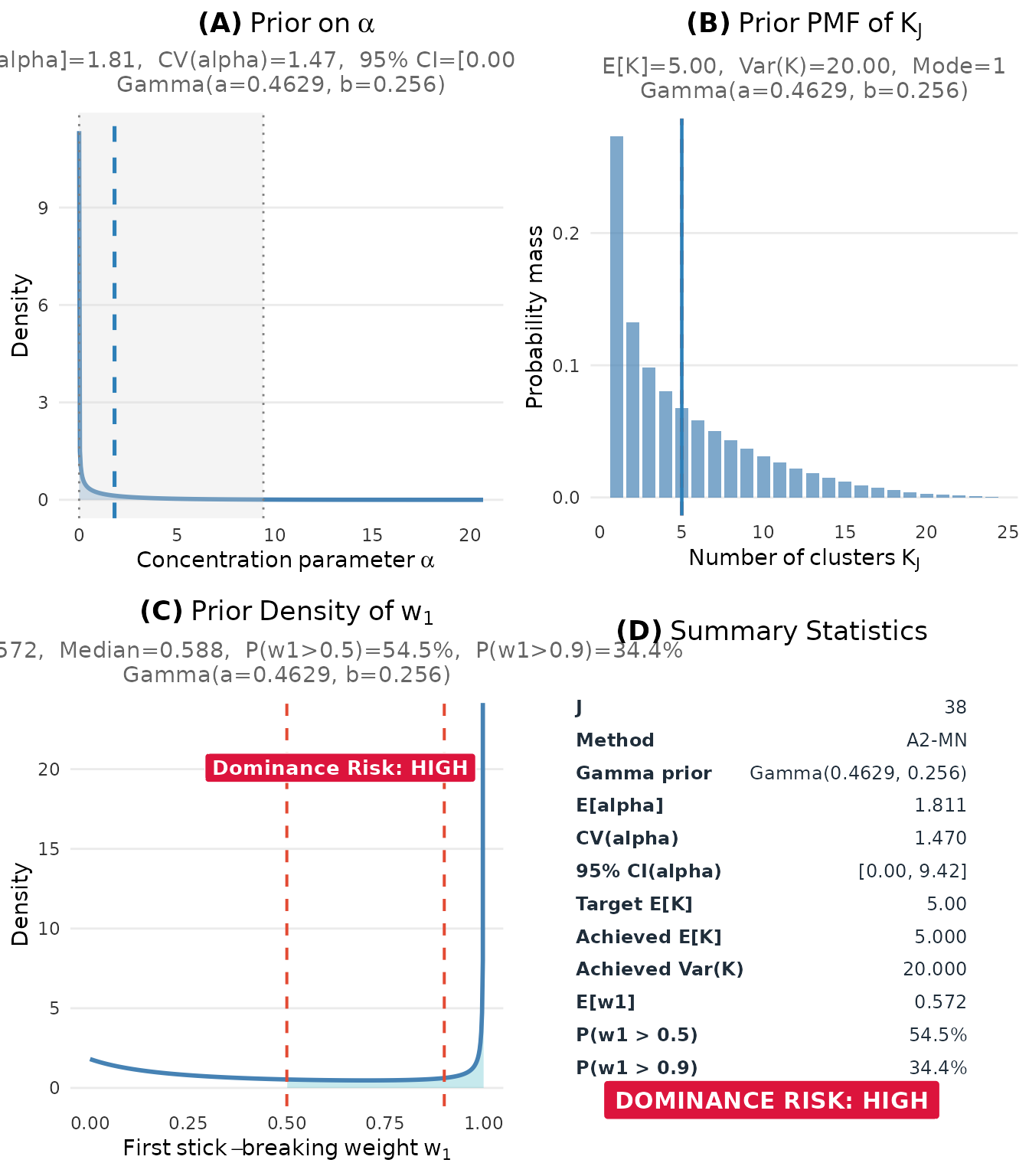

Complete prior elicitation dashboard for the CCT multisite trial (J = 38, μ_K = 5).

#> TableGrob (2 x 2) "dpprior_dashboard": 4 grobs
#>   z     cells              name           grob
#> 1 1 (1-1,1-1) dpprior_dashboard gtable[layout]
#> 2 2 (2-2,1-1) dpprior_dashboard gtable[layout]
#> 3 3 (1-1,2-2) dpprior_dashboard gtable[layout]
#> 4 4 (2-2,2-2) dpprior_dashboard gtable[layout]

1.6 Addressing the Dominance Problem

The diagnostics reveal an important concern: high dominance risk with $P(w_1 > 0.5) = 0.54$ . This means there is a 54% prior probability that a single cluster contains more than half of all sites.

In a setting with limited between-site information, this high dominance probability can lead to overshrinkage in posterior inference. The dual-anchor framework allows us to constrain the prior to reduce dominance while maintaining our beliefs about the expected number of clusters.

Applying dual-anchor refinement:

We target $P(w_1 > 0.5) = 0.25$ (25% dominance probability) while keeping $K$ as the primary anchor ( $\lambda = 0.7$ ):

# Apply dual-anchor to reduce dominance risk
fit_cct_dual <- DPprior_dual(
  fit = fit_cct,
  w1_target = list(prob = list(threshold = 0.5, value = 0.25)),
  lambda = 0.7,  # K remains primary anchor
  loss_type = "adaptive",
  verbose = FALSE
)

cat("Original prior:    Gamma(a =", round(fit_cct$a, 4), 
    ", b =", round(fit_cct$b, 4), ")\n")
#> Original prior:    Gamma(a = 0.4629 , b = 0.2556 )
cat("Dual-anchor prior: Gamma(a =", round(fit_cct_dual$a, 4), 
    ", b =", round(fit_cct_dual$b, 4), ")\n")
#> Dual-anchor prior: Gamma(a = 1.0887 , b = 0.4362 )

Verifying the improvement:

diag_cct_dual <- DPprior_diagnostics(fit_cct_dual)

# Create comparison table
comparison_df <- data.frame(
  Metric = c("E[α]", "E[K]", "Var(K)", "E[w₁]", "P(w₁ > 0.5)", "Dominance Risk"),
  Original = c(
    round(diag_cct$alpha$mean, 3),
    round(diag_cct$K$mean, 2),
    round(diag_cct$K$var, 2),
    round(diag_cct$weights$mean, 3),
    round(diag_cct$weights$prob_exceeds["prob_gt_0.5"], 3),
    diag_cct$weights$dominance_risk
  ),
  Dual_Anchor = c(
    round(diag_cct_dual$alpha$mean, 3),
    round(diag_cct_dual$K$mean, 2),
    round(diag_cct_dual$K$var, 2),
    round(diag_cct_dual$weights$mean, 3),
    round(diag_cct_dual$weights$prob_exceeds["prob_gt_0.5"], 3),
    diag_cct_dual$weights$dominance_risk
  )
)

knitr::kable(
  comparison_df,
  col.names = c("Metric", "K-only Prior", "Dual-Anchor Prior"),
  caption = "Comparison of K-only and dual-anchor priors for the CCT study"
)

Comparison of K-only and dual-anchor priors for the CCT study
Metric	K-only Prior	Dual-Anchor Prior
E[α]	1.811	2.496
E[K]	5	6.65
Var(K)	20	18
E[w₁]	0.572	0.41
P(w₁ > 0.5)	0.545	0.355
Dominance Risk	high	moderate

1.7 Comparing K-only vs Dual-Anchor Priors

Let’s visualize the difference between the two priors:

# Prepare data for K PMF comparison
logS_cct <- compute_log_stirling(J_cct)

pmf_original <- pmf_K_marginal(J_cct, fit_cct$a, fit_cct$b, logS = logS_cct)
pmf_dual <- pmf_K_marginal(J_cct, fit_cct_dual$a, fit_cct_dual$b, logS = logS_cct)

k_compare_df <- data.frame(
  K = rep(seq_along(pmf_original), 2),
  Probability = c(pmf_original, pmf_dual),
  Prior = rep(c("K-only", "Dual-anchor"), each = length(pmf_original))
)
k_compare_df$Prior <- factor(k_compare_df$Prior, levels = c("K-only", "Dual-anchor"))

# Prepare data for w1 comparison
w1_grid <- seq(0, 1, length.out = 200)
w1_dens_original <- sapply(w1_grid, function(w) density_w1(w, fit_cct$a, fit_cct$b))
w1_dens_dual <- sapply(w1_grid, function(w) density_w1(w, fit_cct_dual$a, fit_cct_dual$b))

w1_compare_df <- data.frame(
  w1 = rep(w1_grid, 2),
  Density = c(w1_dens_original, w1_dens_dual),
  Prior = rep(c("K-only", "Dual-anchor"), each = length(w1_grid))
)
w1_compare_df$Prior <- factor(w1_compare_df$Prior, levels = c("K-only", "Dual-anchor"))

# Create plots
p1 <- ggplot(k_compare_df[k_compare_df$K <= 15, ], 
             aes(x = K, y = Probability, fill = Prior)) +
  geom_col(position = "dodge", alpha = 0.8) +
  scale_fill_manual(values = palette_2) +
  labs(
    x = expression(K[J]),
    y = "Probability",
    title = "Cluster Count Distribution"
  ) +
  theme_minimal() +
  theme(legend.position = "bottom", legend.title = element_blank())

p2 <- ggplot(w1_compare_df, aes(x = w1, y = Density, color = Prior)) +
  geom_line(linewidth = 1) +
  geom_vline(xintercept = 0.5, linetype = "dashed", color = "gray50") +
  scale_color_manual(values = palette_2) +
  labs(
    x = expression(w[1]),
    y = "Density",
    title = "Largest Cluster Weight Distribution"
  ) +
  theme_minimal() +
  theme(legend.position = "bottom", legend.title = element_blank())

gridExtra::grid.arrange(p1, p2, ncol = 2)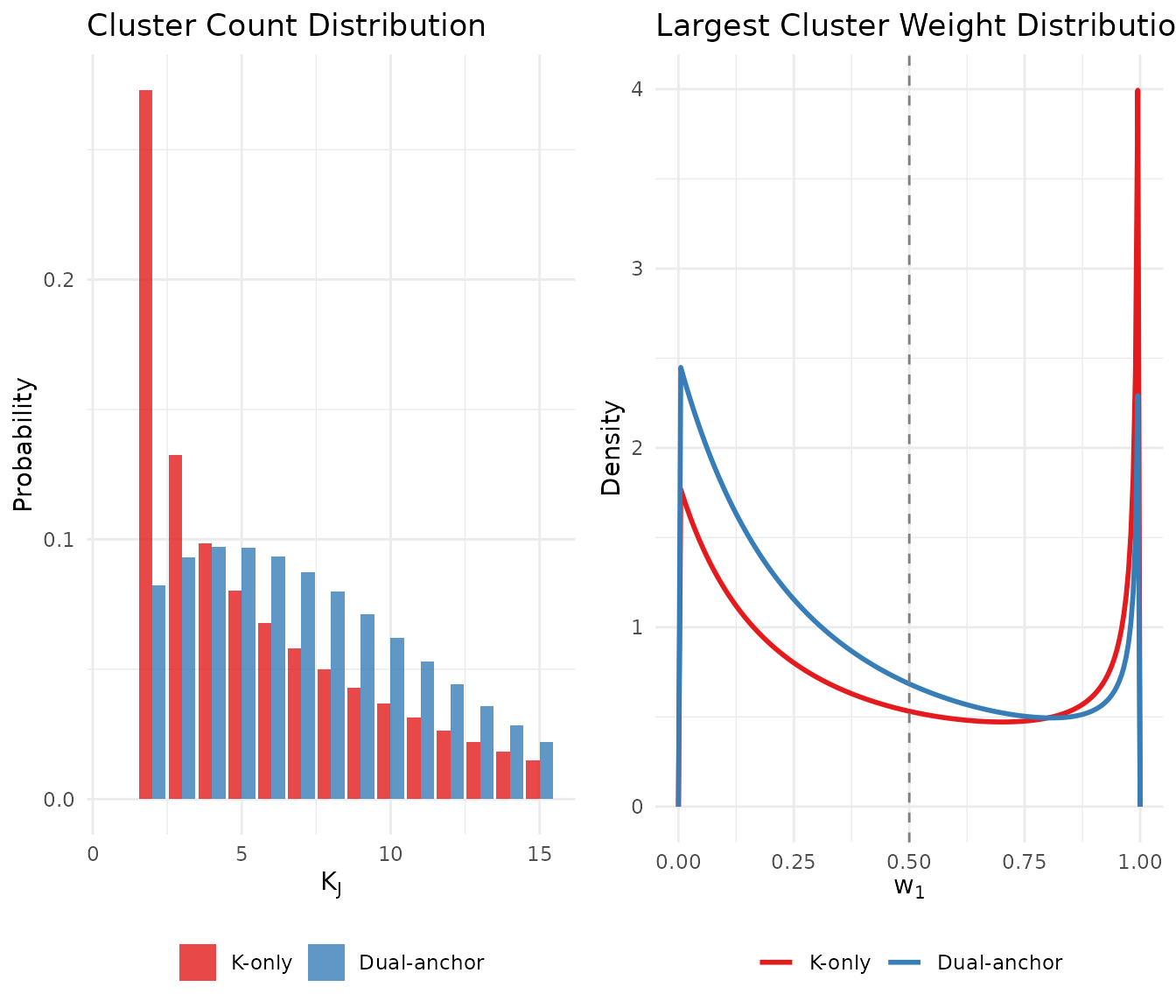

Comparison of K-only and dual-anchor priors: the dual-anchor approach reduces dominance risk while maintaining similar cluster count expectations.

The dual-anchor prior shifts mass in the $w_1$ distribution away from extreme values (right panel) while maintaining a similar expected number of clusters (left panel). This achieves our goal of reducing dominance risk without substantially changing our beliefs about cluster count.

1.8 Sensitivity Analysis

Given the uncertainty in our prior specification, we conduct a sensitivity analysis across a range of plausible values for both the K-only and dual-anchor approaches:

# Sensitivity to μ_K
mu_K_grid <- c(3, 5, 7, 10)

sensitivity_results <- lapply(mu_K_grid, function(mu) {
  # K-only fit
  fit_k <- DPprior_fit(J = J_cct, mu_K = mu, confidence = "low")
  diag_k <- DPprior_diagnostics(fit_k)
  
  # Dual-anchor fit
  fit_d <- DPprior_dual(
    fit = fit_k,
    w1_target = list(prob = list(threshold = 0.5, value = 0.25)),
    lambda = 0.7,
    loss_type = "adaptive",
    verbose = FALSE
  )
  diag_d <- DPprior_diagnostics(fit_d)
  
  data.frame(
    mu_K = mu,
    # K-only results
    a_k = round(fit_k$a, 3),
    b_k = round(fit_k$b, 3),
    E_K_k = round(diag_k$K$mean, 2),
    P_dom_k = round(diag_k$weights$prob_exceeds["prob_gt_0.5"], 3),
    # Dual-anchor results
    a_d = round(fit_d$a, 3),
    b_d = round(fit_d$b, 3),
    E_K_d = round(diag_d$K$mean, 2),
    P_dom_d = round(diag_d$weights$prob_exceeds["prob_gt_0.5"], 3)
  )
})
#> Warning: HIGH DOMINANCE RISK: P(w1 > 0.5) = 74.3% exceeds 40%.
#>   This may indicate unintended prior behavior (RN-07).
#>   Consider using DPprior_dual() for weight-constrained elicitation.
#>   See ?DPprior_diagnostics for interpretation.
#> Warning: HIGH DOMINANCE RISK: P(w1 > 0.5) = 54.5% exceeds 40%.
#>   This may indicate unintended prior behavior (RN-07).
#>   Consider using DPprior_dual() for weight-constrained elicitation.
#>   See ?DPprior_diagnostics for interpretation.

sensitivity_df <- do.call(rbind, sensitivity_results)

knitr::kable(
  sensitivity_df,
  col.names = c("Target μ_K", 
                "a (K)", "b (K)", "E[K]", "P(w₁>0.5)",
                "a (DA)", "b (DA)", "E[K]", "P(w₁>0.5)"),
  row.names = FALSE,
  caption = "Sensitivity analysis: K-only (K) vs Dual-anchor (DA) priors (J = 38, low confidence)"
)

Sensitivity analysis: K-only (K) vs Dual-anchor (DA) priors (J = 38, low confidence)
Target μ_K	a (K)	b (K)	E[K]	P(w₁>0.5)	a (DA)	b (DA)	E[K]	P(w₁>0.5)
3	0.270	0.345	3	0.743	7.568	3.733	6.45	0.276
5	0.463	0.256	5	0.545	1.089	0.436	6.65	0.355
7	0.601	0.191	7	0.399	0.840	0.232	7.94	0.313
10	0.727	0.123	10	0.253	0.732	0.124	10.03	0.251

1.9 Final Prior Selection and Reporting

Based on our analysis, we recommend the dual-anchor prior for the CCT study, as it provides appropriate control over dominance risk in this low between-site information setting.

cat("RECOMMENDED PRIOR FOR CCT STUDY\n")
#> RECOMMENDED PRIOR FOR CCT STUDY
cat("================================\n")
#> ================================
cat("α ~ Gamma(", round(fit_cct_dual$a, 4), ", ", round(fit_cct_dual$b, 4), ")\n\n", sep = "")
#> α ~ Gamma(1.0887, 0.4362)
cat("Key properties:\n")
#> Key properties:
cat("  E[K] =", round(diag_cct_dual$K$mean, 2), "clusters\n")
#>   E[K] = 6.65 clusters
cat("  P(w₁ > 0.5) =", round(diag_cct_dual$weights$prob_exceeds["prob_gt_0.5"], 2), "\n")
#>   P(w₁ > 0.5) = 0.36
cat("  Dominance risk:", diag_cct_dual$weights$dominance_risk, "\n")
#>   Dominance risk: moderate

Reporting language for publication:

We elicited beliefs about the number of latent clusters among the $J = 38$ sites in the CCT multisite trial. Based on substantive knowledge of similar education interventions and the uniformity of implementation, we specified $\mathbb{E}[K_J] = 5$ (approximately five distinct response patterns) with low confidence. Initial diagnostics using the K-only calibration revealed high dominance risk with $P(w_1 > 0.5) = 0.54$ , which is problematic in settings with limited between-site information. We therefore applied dual-anchor refinement targeting $P(w_1 > 0.5) \leq 0.25$ with $\lambda = 0.7$ , yielding a Gamma(1.089, 0.436) hyperprior. The refined prior maintains $\mathbb{E}[K_J] \approx 6.7$ while reducing dominance risk to moderate. Sensitivity analyses across $\mu_K \in \{3, 5, 7, 10\}$ confirmed that substantive conclusions were robust to prior specification.

2. Case Study: Brief Alcohol Interventions Meta-Analysis

2.1 Research Context

Our second case study is based on the meta-analysis of brief alcohol interventions (BAI) for adolescents and young adults conducted by Pustejovsky & Tipton (2022), who re-analyzed data from Tanner-Smith & Lipsey (2015).

Study characteristics:

Number of studies: 117 randomized trials
Total effect sizes: 1,198 estimates
Effect sizes per study: Median = 6, range = 1 to 108
Outcome: Alcohol consumption (standardized mean differences)
Key feature: Complex dependence structure (correlated and hierarchical)

2.2 The Meta-Analytic Challenge

In meta-analysis, the Dirichlet Process mixture model can be used to flexibly model the distribution of true study effects. This is particularly valuable when:

The true effect distribution may be non-Gaussian
There may be discrete subpopulations of studies with similar effects
Robust inference is needed without strong distributional assumptions

The BAI meta-analysis presents a setting with substantial between-study heterogeneity ( $\hat{\tau} = 0.182$ under the correlated effects model), suggesting the potential for distinct effect subgroups.

2.3 Eliciting the Prior

Step 1: Substantive reasoning about clusters

In the BAI context, we consider potential sources of effect heterogeneity:

Intervention type: Brief motivational interviewing vs. feedback-only vs. multi-session programs vs. computerized interventions
Population: College students vs. high school vs. clinical samples vs. community populations
Outcome timing: Immediate vs. short-term (3 months) vs. medium-term (6 months) vs. long-term (12+ months) effects
Control condition: No treatment vs. attention control vs. treatment-as-usual vs. alternative intervention
Delivery format: Individual vs. group vs. self-administered
Setting: Healthcare vs. educational vs. community

Given the many potential mechanisms for heterogeneity and the large number of studies, a reasonable expectation might be 15–25 distinct effect clusters among 117 studies. We start with $\mu_K = 18$ :

# Define the meta-analysis context
J_bai <- 117
mu_K_bai <- 18

cat("Meta-analysis context:\n")
#> Meta-analysis context:
cat("  Number of studies (J):", J_bai, "\n")
#>   Number of studies (J): 117
cat("  Expected clusters (μ_K):", mu_K_bai, "\n")
#>   Expected clusters (μ_K): 18
cat("  Ratio (μ_K/J):", round(mu_K_bai / J_bai, 3), "\n")
#>   Ratio (μ_K/J): 0.154

Step 2: Expressing uncertainty

Meta-analyses often have more uncertainty about the number of distinct effect clusters than multisite trials, as studies are conducted independently with varying methodologies. We use low confidence:

fit_bai <- DPprior_fit(
  J = J_bai, 
  mu_K = mu_K_bai, 
  confidence = "low"
)

print(fit_bai)
#> DPprior Prior Elicitation Result
#> ============================================= 
#> 
#> Gamma Hyperprior: α ~ Gamma(a = 1.9005, b = 0.2986)
#>   E[α] = 6.365, SD[α] = 4.617
#> 
#> Target (J = 117):
#>   E[K_J]   = 18.00
#>   Var(K_J) = 85.00
#>   (from confidence = 'low')
#> 
#> Achieved:
#>   E[K_J] = 18.000000, Var(K_J) = 85.000000
#>   Residual = 2.16e-12
#> 
#> Method: A2-MN (6 iterations)
#> 
#> Dominance Risk: LOW ✓ (P(w₁>0.5) = 10%)

Step 3: Diagnostic verification

diag_bai <- DPprior_diagnostics(fit_bai)

cat("Diagnostic Summary:\n")
#> Diagnostic Summary:
cat("----------------\n")
#> ----------------
cat("Alpha distribution:\n")
#> Alpha distribution:
cat("  E[α] =", round(diag_bai$alpha$mean, 3), "\n")
#>   E[α] = 6.365
cat("  SD(α) =", round(diag_bai$alpha$sd, 3), "\n")
#>   SD(α) = 4.617
cat("  95% CI: [", round(diag_bai$alpha$quantiles["q5"], 3), ", ",
    round(diag_bai$alpha$quantiles["q95"], 3), "]\n", sep = "")
#>   95% CI: [1.059, 15.344]
cat("\nCluster count:\n")
#> 
#> Cluster count:
cat("  E[K] =", round(diag_bai$K$mean, 3), "\n")
#>   E[K] = 18
cat("  Var(K) =", round(diag_bai$K$var, 3), "\n")
#>   Var(K) = 85
cat("  Mode(K) =", diag_bai$K$mode, "\n")
#>   Mode(K) = 14
cat("\nWeight behavior:\n")
#> 
#> Weight behavior:
cat("  E[w₁] =", round(diag_bai$weights$mean, 3), "\n")
#>   E[w₁] = 0.2
cat("  P(w₁ > 0.5) =", 
    round(diag_bai$weights$prob_exceeds["prob_gt_0.5"], 3), "\n")
#>   P(w₁ > 0.5) = 0.102
cat("  Dominance risk:", diag_bai$weights$dominance_risk, "\n")
#>   Dominance risk: low

2.4 Comparing Alternative Specifications

For meta-analysis, it is valuable to compare different prior specifications to assess robustness. We compare three approaches: expecting fewer clusters, the baseline, and expecting more clusters.

# Define three candidate priors
bai_candidates <- list(
  "Conservative (μ_K = 10)" = DPprior_fit(J = J_bai, mu_K = 10, confidence = "low"),
  "Baseline (μ_K = 18)" = DPprior_fit(J = J_bai, mu_K = 18, confidence = "low"),
  "Liberal (μ_K = 30)" = DPprior_fit(J = J_bai, mu_K = 30, confidence = "low")
)

# Create comparison table
bai_comp_results <- lapply(names(bai_candidates), function(nm) {
  fit <- bai_candidates[[nm]]
  diag <- DPprior_diagnostics(fit)
  data.frame(
    Prior = nm,
    a = round(fit$a, 3),
    b = round(fit$b, 3),
    E_K = round(diag$K$mean, 2),
    E_w1 = round(diag$weights$mean, 3),
    E_rho = round(diag$coclustering$mean, 3)
  )
})

bai_comp_df <- do.call(rbind, bai_comp_results)

knitr::kable(
  bai_comp_df,
  col.names = c("Prior", "a", "b", "E[K]", "E[w₁]", "E[ρ]"),
  caption = "Comparison of candidate priors for the BAI meta-analysis (J = 117)"
)

Comparison of candidate priors for the BAI meta-analysis (J = 117)
Prior	a	b	E[K]	E[w₁]	E[ρ]
Conservative (μ_K = 10)	1.232	0.449	10	0.379	0.379
Baseline (μ_K = 18)	1.901	0.299	18	0.200	0.200
Liberal (μ_K = 30)	2.470	0.173	30	0.096	0.096

2.5 Visualizing the Comparison

# Create data for K PMF comparison
logS_bai <- compute_log_stirling(J_bai)

k_bai_df <- do.call(rbind, lapply(names(bai_candidates), function(nm) {
  fit <- bai_candidates[[nm]]
  pmf <- pmf_K_marginal(J_bai, fit$a, fit$b, logS = logS_bai)
  data.frame(
    K = seq_along(pmf),
    probability = pmf,
    Prior = nm
  )
}))
k_bai_df$Prior <- factor(k_bai_df$Prior, levels = names(bai_candidates))

# Plot PMF comparison
ggplot(k_bai_df[k_bai_df$K <= 50, ], 
       aes(x = K, y = probability, color = Prior)) +
  geom_line(linewidth = 0.8) +
  geom_point(size = 1.5) +
  scale_color_manual(values = palette_3) +
  labs(
    x = expression(K[J]),
    y = "Probability",
    title = "Prior PMF of Number of Clusters (BAI Meta-Analysis)",
    subtitle = "J = 117 studies"
  ) +
  theme_minimal() +
  theme(legend.position = "bottom", legend.title = element_blank())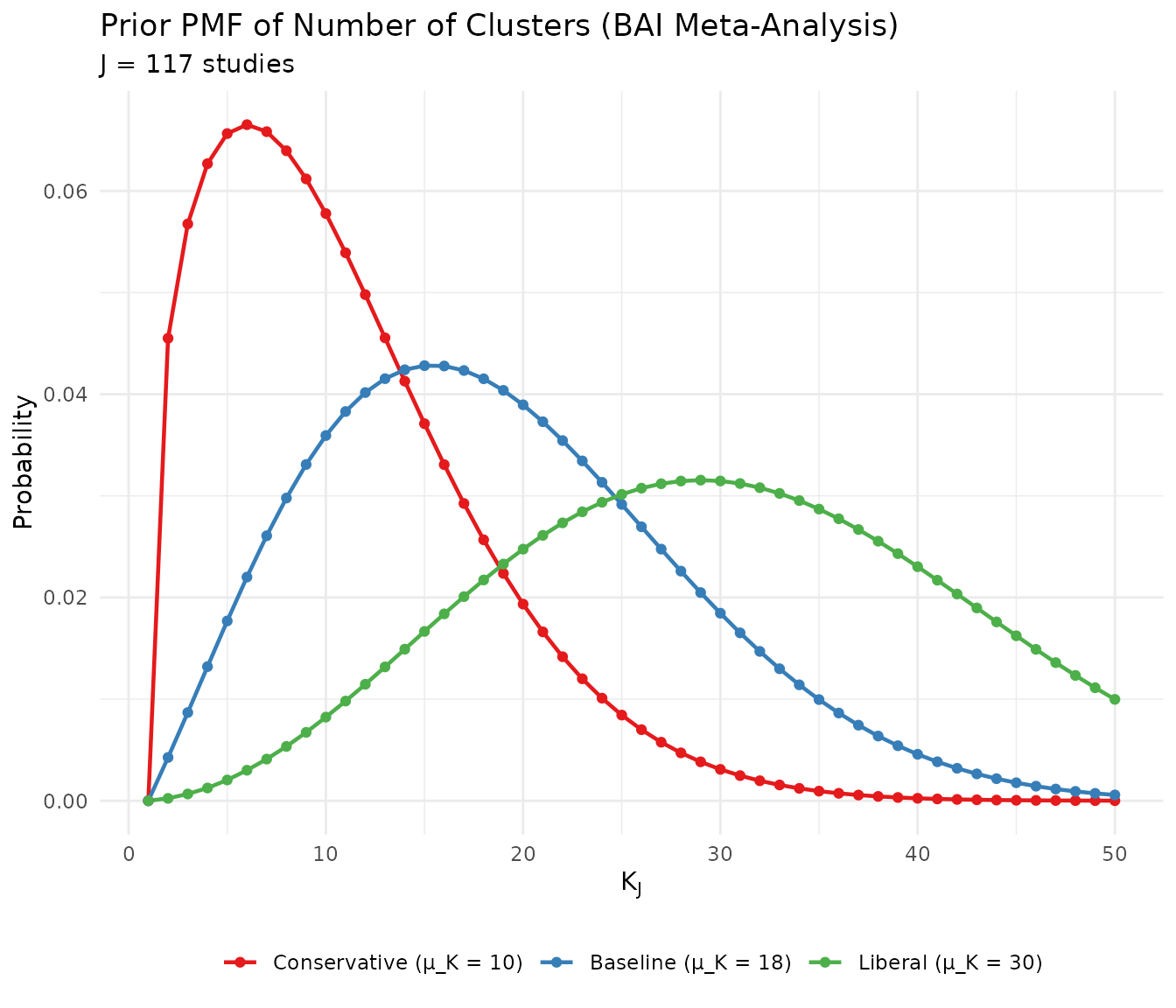

Comparison of three candidate priors for the BAI meta-analysis.

3. Case Study: Alabama Pre-K Value-Added Analysis

3.1 Research Context

Our third case study illustrates prior elicitation for a large-scale value-added analysis in Alabama’s pre-kindergarten program.

Study characteristics:

Sites: 847 pre-K sites across the state
Providers: 74.4% public schools, 10.4% private centers, 6.2% Head Start, and others
Class sizes: 13–18 students per classroom
Outcomes: Six developmental domains (Literacy, Mathematics, Cognitive, Language, Social-Emotional, Physical)
Assessment: Teaching Strategies GOLD®

A note on package limitations: The current version of DPprior supports $J \leq 500$ due to pre-computed unsigned Stirling numbers of the first kind, which are required for exact moment calculations. Support for larger $J$ is planned for future releases. For the 847 sites in the Alabama study, we demonstrate the workflow using $J = 500$ as a practical upper bound. This limitation has minimal impact on substantive conclusions for several reasons: (1) the relationship between $\alpha$ and $\mathbb{E}[K_J]$ is approximately logarithmic in $J$ , so results are relatively stable across nearby sample sizes; (2) using a conservative (smaller) $J$ tends to produce slightly more concentrated priors, which is a defensible choice in uncertain settings; and (3) the $\mu_K / J$ ratio—rather than $J$ alone—is the primary driver of the elicited prior.

3.2 The Value-Added Challenge

Value-added models (VAMs) estimate site-specific contributions to student learning ( $\theta_j$ ). Key challenges in this context include:

Distribution estimation: Is the distribution of site effects normal, or are there distinct subpopulations?
Tail identification: Which sites fall in the lowest and highest 10% of the distribution?
Ranking: Can we produce meaningful “report cards” for sites?

The semiparametric Dirichlet Process approach allows flexible modeling of the site effect distribution without imposing normality.

3.3 Eliciting the Prior

Step 1: Substantive considerations

With 847 sites, we expect considerable heterogeneity. Potential sources of clustering include:

Provider type: Public schools vs. private centers vs. Head Start may exhibit systematically different effects
Geographic region: Urban vs. rural patterns
Resource levels: Varying levels of site resources and teacher qualifications
Implementation fidelity: Variation in how the curriculum is delivered

A reasonable expectation might be 40–60 distinct “types” of sites, representing approximately 5–7% of the total. We specify $\mu_K = 50$ :

# Define the context
# Note: Using J = 500 (package maximum) for the 847-site study
J_alabama <- 500
mu_K_alabama <- 50

cat("Alabama Pre-K context:\n")
#> Alabama Pre-K context:
cat("  Actual number of sites: 847\n")
#>   Actual number of sites: 847
cat("  J used for elicitation:", J_alabama, "(package maximum)\n")
#>   J used for elicitation: 500 (package maximum)
cat("  Expected clusters (μ_K):", mu_K_alabama, "\n")
#>   Expected clusters (μ_K): 50
cat("  Ratio (μ_K/J):", round(mu_K_alabama / J_alabama, 3), "\n")
#>   Ratio (μ_K/J): 0.1

Step 2: Prior elicitation

# Fit using A2-MN method
fit_alabama <- DPprior_fit(
  J = J_alabama, 
  mu_K = mu_K_alabama, 
  confidence = "low",
  method = "A2-MN"
)

print(fit_alabama)
#> DPprior Prior Elicitation Result
#> ============================================= 
#> 
#> Gamma Hyperprior: α ~ Gamma(a = 6.2200, b = 0.4431)
#>   E[α] = 14.038, SD[α] = 5.629
#> 
#> Target (J = 500):
#>   E[K_J]   = 50.00
#>   Var(K_J) = 245.00
#>   (from confidence = 'low')
#> 
#> Achieved:
#>   E[K_J] = 50.000000, Var(K_J) = 245.000000
#>   Residual = 2.84e-14
#> 
#> Method: A2-MN (6 iterations)
#> 
#> Dominance Risk: LOW ✓ (P(w₁>0.5) = 0%)

Step 3: Diagnostics

diag_alabama <- DPprior_diagnostics(fit_alabama)

cat("Diagnostic Summary:\n")
#> Diagnostic Summary:
cat("----------------\n")
#> ----------------
cat("Alpha distribution:\n")
#> Alpha distribution:
cat("  E[α] =", round(diag_alabama$alpha$mean, 3), "\n")
#>   E[α] = 14.038
cat("  SD(α) =", round(diag_alabama$alpha$sd, 3), "\n")
#>   SD(α) = 5.629
cat("  95% CI: [", round(diag_alabama$alpha$quantiles["q5"], 3), ", ",
    round(diag_alabama$alpha$quantiles["q95"], 3), "]\n", sep = "")
#>   95% CI: [6.226, 24.392]
cat("\nCluster count:\n")
#> 
#> Cluster count:
cat("  E[K] =", round(diag_alabama$K$mean, 2), "\n")
#>   E[K] = 50
cat("  SD(K) =", round(sqrt(diag_alabama$K$var), 2), "\n")
#>   SD(K) = 15.65
cat("\nWeight behavior:\n")
#> 
#> Weight behavior:
cat("  E[w₁] =", round(diag_alabama$weights$mean, 4), "\n")
#>   E[w₁] = 0.077
cat("  P(w₁ > 0.5) =", 
    round(diag_alabama$weights$prob_exceeds["prob_gt_0.5"], 4), "\n")
#>   P(w₁ > 0.5) = 0.0029
cat("  Dominance risk:", diag_alabama$weights$dominance_risk, "\n")
#>   Dominance risk: low

3.4 Sensitivity Analysis

We examine how the elicited prior changes across different specifications:

# Sensitivity to μ_K
mu_K_grid <- c(30, 40, 50, 60, 75)

sensitivity_alabama <- lapply(mu_K_grid, function(mu) {
  fit <- DPprior_fit(J = J_alabama, mu_K = mu, confidence = "low", method = "A2-MN")
  diag <- DPprior_diagnostics(fit)
  data.frame(
    mu_K = mu,
    ratio = round(mu / J_alabama, 3),
    a = round(fit$a, 3),
    b = round(fit$b, 3),
    E_K = round(diag$K$mean, 1),
    P_dom = round(diag$weights$prob_exceeds["prob_gt_0.5"], 4)
  )
})

sensitivity_alabama_df <- do.call(rbind, sensitivity_alabama)

knitr::kable(
  sensitivity_alabama_df,
  col.names = c("Target μ_K", "μ_K/J", "a", "b", "E[K]", "P(w₁ > 0.5)"),
  caption = "Sensitivity analysis for the Alabama Pre-K study (J = 500)"
)

Sensitivity analysis for the Alabama Pre-K study (J = 500)
	Target μ_K	μ_K/J	a	b	E[K]	P(w₁ > 0.5)
prob_gt_0.5	30	0.06	4.171	0.588	30	0.0388
prob_gt_0.51	40	0.08	5.252	0.506	40	0.0108
prob_gt_0.52	50	0.10	6.220	0.443	50	0.0029
prob_gt_0.53	60	0.12	7.087	0.392	60	0.0007
prob_gt_0.54	75	0.15	8.215	0.330	75	0.0001

3.5 Visualizing Prior Behavior

# Plot alpha and K distributions side by side
# Alpha distribution
alpha_grid <- seq(0.01, 25, length.out = 300)
alpha_df <- data.frame(
  alpha = alpha_grid,
  density = dgamma(alpha_grid, shape = fit_alabama$a, rate = fit_alabama$b)
)

p1 <- ggplot(alpha_df, aes(x = alpha, y = density)) +
  geom_line(linewidth = 1, color = "#377EB8") +
  geom_vline(xintercept = diag_alabama$alpha$mean, 
             linetype = "dashed", color = "gray40") +
  annotate("text", x = diag_alabama$alpha$mean + 1.5, y = max(alpha_df$density) * 0.9,
           label = sprintf("E[α] = %.1f", diag_alabama$alpha$mean),
           hjust = 0, color = "gray40") +
  labs(
    x = expression(alpha),
    y = "Density",
    title = expression("Prior on " * alpha)
  ) +
  theme_minimal()

# K distribution
logS_al <- compute_log_stirling(J_alabama)
pmf_K <- pmf_K_marginal(J_alabama, fit_alabama$a, fit_alabama$b, logS = logS_al)
k_df <- data.frame(
  K = seq_along(pmf_K),
  probability = pmf_K
)

p2 <- ggplot(k_df[k_df$K <= 100 & k_df$probability > 1e-4, ], 
             aes(x = K, y = probability)) +
  geom_col(fill = "#377EB8", alpha = 0.7) +
  geom_vline(xintercept = diag_alabama$K$mean, 
             linetype = "dashed", color = "gray40") +
  annotate("text", x = diag_alabama$K$mean + 5, y = max(k_df$probability) * 0.9,
           label = sprintf("E[K] = %.0f", diag_alabama$K$mean),
           hjust = 0, color = "gray40") +
  labs(
    x = expression(K[J]),
    y = "Probability",
    title = expression("Prior PMF of " * K[J])
  ) +
  theme_minimal()

gridExtra::grid.arrange(p1, p2, ncol = 2)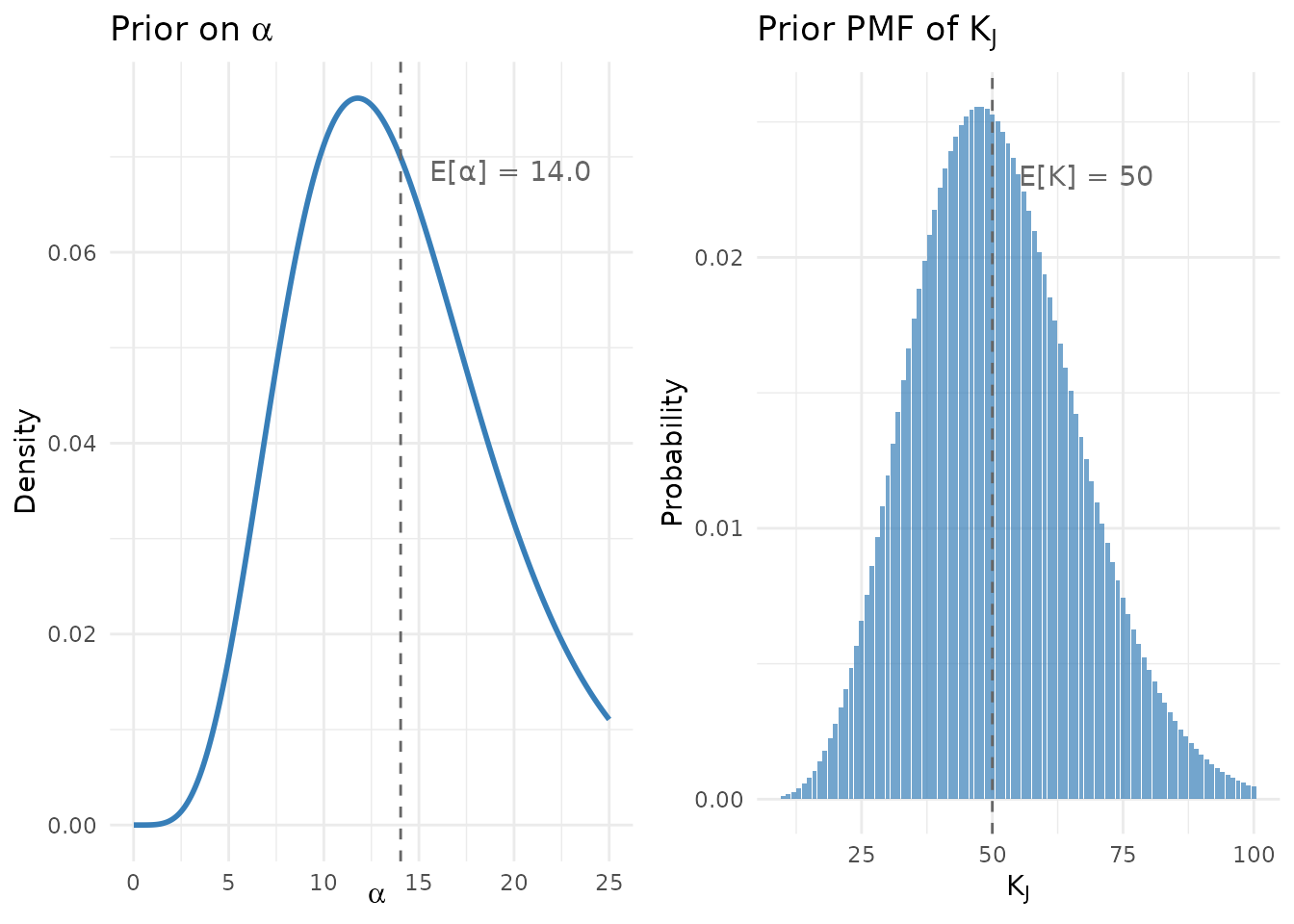

Prior distributions for the Alabama Pre-K study (J = 500, μ_K = 50).

4. Reporting Prior Elicitation in Publications

4.1 Key Elements to Report

When reporting prior elicitation in a publication, include:

Study context: Number of units ( $J$ ) and their nature
Substantive rationale: Why you expect a certain number of clusters
Uncertainty characterization: Confidence level or variance specification
Algorithm used: A1, A2-MN, or A2-KL
Resulting hyperparameters: The $\text{Gamma}(a, b)$ specification
Diagnostic summary: Key quantities like $P(w_1 > 0.5)$ and dominance risk
Sensitivity analysis: Results for alternative specifications

Summary

This vignette demonstrated how to apply the DPprior package across three diverse research contexts:

Case Study	J	μ_K	Key Insight
CCT Multisite Trial	38	5	Dual-anchor refinement essential for low-information settings
BAI Meta-Analysis	117	18	Multiple heterogeneity sources suggest more clusters
Alabama Pre-K VAM	500	50	Large-scale applications work within package limits

Key Takeaways:

Context matters: The appropriate $\mu_K$ depends on substantive domain knowledge about heterogeneity sources
Diagnostics are essential: Always verify weight behavior, not just cluster counts
Dual-anchor refinement: When dominance risk is high, use DPprior_dual() to control weight behavior
Sensitivity analysis is mandatory: Report results across plausible alternative specifications
Transparent reporting: Document the complete elicitation process in publications

References

Barrera-Osorio, F., Linden, L. L., & Saavedra, J. E. (2019). Medium- and long-term educational consequences of alternative conditional cash transfer designs: Experimental evidence from Colombia. American Economic Journal: Applied Economics, 11(3), 54–91. https://doi.org/10.1257/app.20170008

Lee, J., Che, J., Rabe-Hesketh, S., Feller, A., & Miratrix, L. (2025). Improving the estimation of site-specific effects and their distribution in multisite trials. Journal of Educational and Behavioral Statistics, 50(5), 731–764. https://doi.org/10.3102/10769986241254286

Pustejovsky, J. E., & Tipton, E. (2022). Meta-analysis with robust variance estimation: Expanding the range of working models. Prevention Science, 23(3), 425–438. https://doi.org/10.1007/s11121-021-01246-3

Tanner-Smith, E. E., & Lipsey, M. W. (2015). Brief alcohol interventions for adolescents and young adults: A systematic review and meta-analysis. Journal of Substance Abuse Treatment, 51, 1–18. https://doi.org/10.1016/j.jsat.2014.09.001

For questions or feedback, please visit the GitHub repository.

JoonHo Lee

2026-01-01

Overview

1. Case Study: Conditional Cash Transfer Multisite Trial

1.1 Research Context

1.2 The Inferential Goals

1.3 Initial Prior Elicitation

1.4 Comprehensive Diagnostics

1.5 Visualizing the Initial Prior

1.6 Addressing the Dominance Problem

1.7 Comparing K-only vs Dual-Anchor Priors

1.8 Sensitivity Analysis

1.9 Final Prior Selection and Reporting

2. Case Study: Brief Alcohol Interventions Meta-Analysis

2.1 Research Context

2.2 The Meta-Analytic Challenge

2.3 Eliciting the Prior

2.4 Comparing Alternative Specifications

2.5 Visualizing the Comparison

3. Case Study: Alabama Pre-K Value-Added Analysis

3.1 Research Context

3.2 The Value-Added Challenge

3.3 Eliciting the Prior

3.4 Sensitivity Analysis

3.5 Visualizing Prior Behavior

4. Reporting Prior Elicitation in Publications

4.1 Key Elements to Report

Summary

References