Working with Latent Distributions

library(IRTsimrel)

Overview

The sim_latentG() function generates latent abilities (person parameters $\theta$ ) for IRT simulation studies. It implements the population model:

$\theta_p \sim G$

where $G$ is a flexible distribution family that can take many different shapes.

This vignette covers:

The pre-standardization principle
Available distribution shapes
Customizing shape parameters
Creating custom mixture distributions
Adding covariate effects
Visualization tools

The Pre-Standardization Principle

A key design feature of sim_latentG() is pre-standardization: every built-in distribution shape is mathematically constructed to have mean 0 and variance 1 before any scaling is applied.

This ensures that:

Changing the shape does not inadvertently change the scale
The sigma parameter directly controls the standard deviation
Comparisons across shapes are meaningful

The generated abilities follow:

$\theta_p = \mu + X_p^\top \beta + \sigma \cdot z_p$

where $z_p \sim G_0$ with $\mathbb{E}[z] = 0$ and $\text{Var}[z] = 1$ .

Why This Matters

In traditional simulation approaches, changing the latent distribution often changes both the shape and the scale simultaneously. For example, switching from $N(0, 1)$ to $\text{Gamma}(4, 1)$ changes not just the shape but also the variance.

With pre-standardization, you can study the effect of distributional shape on IRT estimation while holding variance constant—a cleaner experimental design.

Basic Usage

# Generate 1000 standard normal abilities
sim_normal <- sim_latentG(n = 1000, shape = "normal", seed = 42)

# Examine the result
print(sim_normal)
#> Latent Ability Distribution (G-family)
#> =======================================
#>   Shape     : normal
#>   n         : 1000
#>   Target mu : 0.000
#>   Target sigma: 1.000
#> 
#> Sample Moments:
#>   Mean      : -0.0258
#>   SD        : 1.0025
#>   Skewness  : -0.0038
#>   Kurtosis  : 0.1286 (excess)

The output shows:

Target mu/sigma: The requested location and scale
Sample Moments: Empirical mean, SD, skewness, and excess kurtosis

# Verify standardization
cat(sprintf("Sample mean: %.4f (target: 0)\n", mean(sim_normal$theta)))
#> Sample mean: -0.0258 (target: 0)
cat(sprintf("Sample SD:   %.4f (target: 1)\n", sd(sim_normal$theta)))
#> Sample SD:   1.0025 (target: 1)

Available Distribution Shapes

sim_latentG() provides 12 built-in shapes, each pre-standardized to mean 0 and variance 1.

Standard Normal

The baseline case: $z \sim N(0, 1)$

sim_normal <- sim_latentG(n = 2000, shape = "normal", seed = 1)
plot(sim_normal, show_normal = TRUE)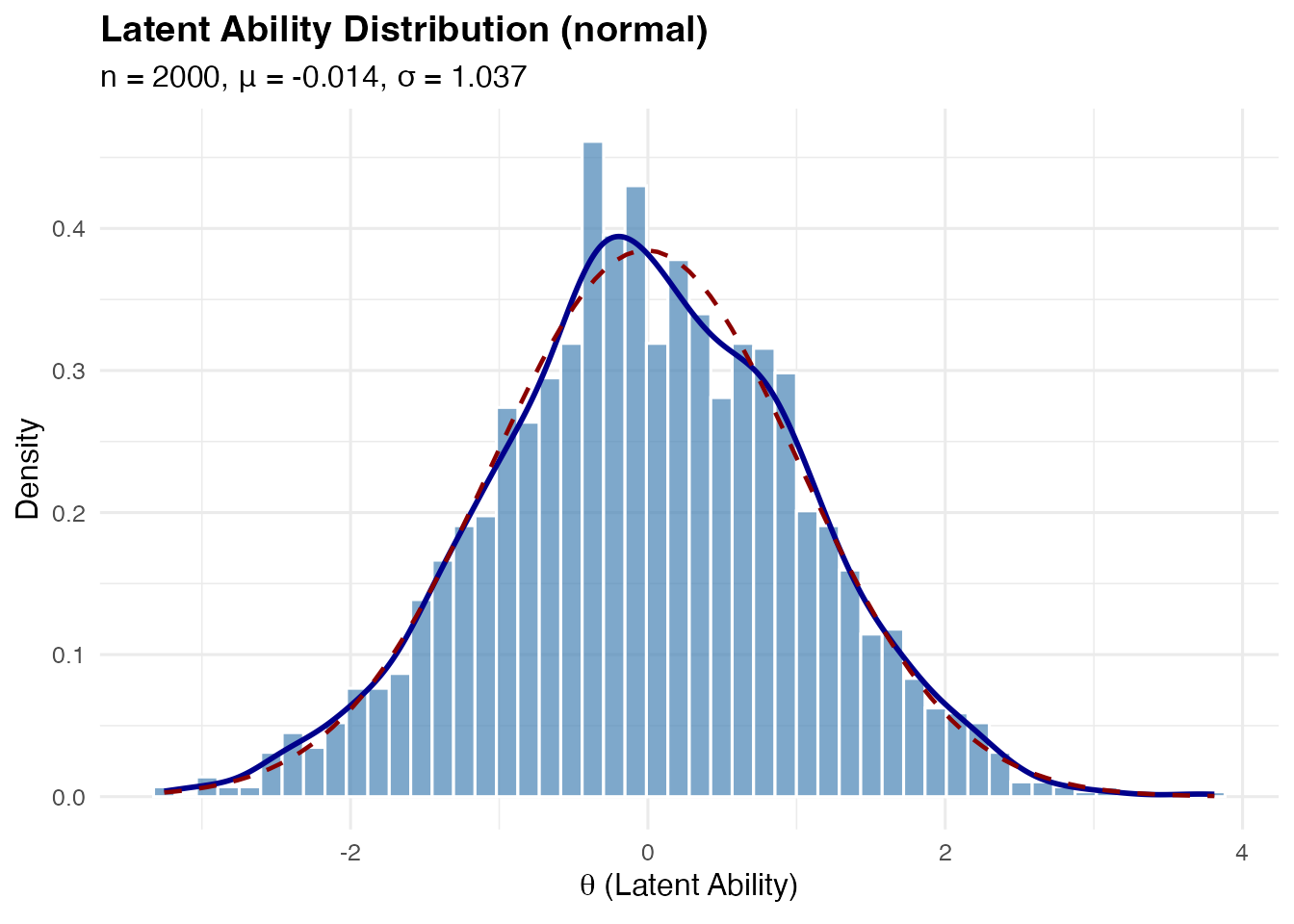

Bimodal Distribution

A symmetric two-component Gaussian mixture, useful for representing populations with two distinct subgroups (e.g., native vs. non-native speakers).

Mathematical construction: $z = s \cdot \delta + \epsilon, \quad s \sim \text{Rademacher}(\pm 1), \quad \epsilon \sim N(0, 1 - \delta^2)$

The component variance $1 - \delta^2$ ensures $\text{Var}[z] = \delta^2 + (1 - \delta^2) = 1$ .

sim_bimodal <- sim_latentG(n = 2000, shape = "bimodal", seed = 1)
plot(sim_bimodal, show_normal = TRUE)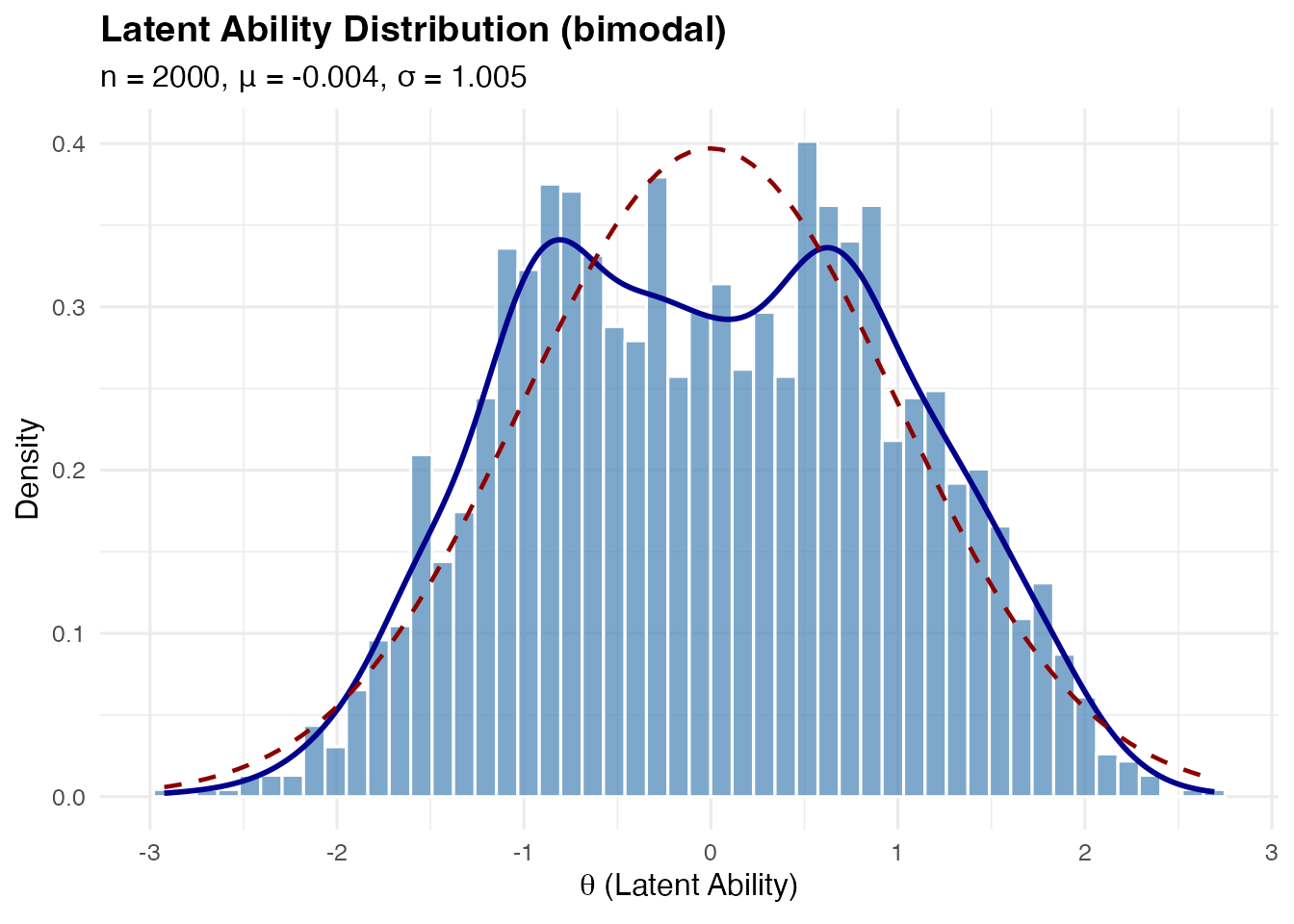

Customizing mode separation:

The delta parameter controls how far apart the modes are (0 < delta < 1):

# Wider separation
sim_bimodal_wide <- sim_latentG(
  n = 2000, 
  shape = "bimodal", 
  shape_params = list(delta = 0.95),
  seed = 1
)
plot(sim_bimodal_wide, show_normal = TRUE)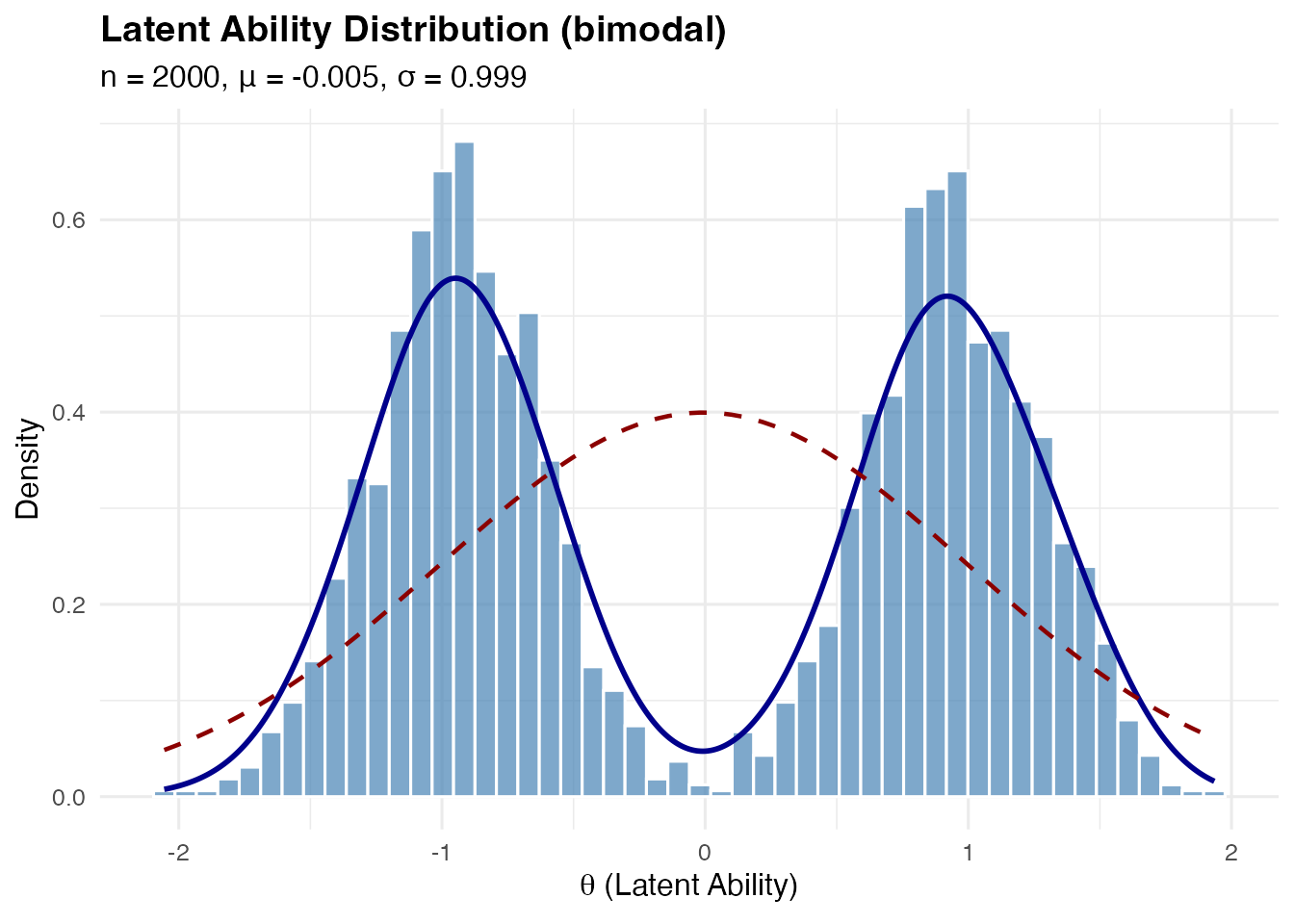

Trimodal Distribution

A symmetric three-component mixture with a central peak and two side peaks.

Mathematical construction:

Components at $\{-m, 0, +m\}$ with weights $(w_L, w_0, w_R)$ where $w_L = w_R = (1 - w_0)/2$ .

Component variance: $\sigma_c^2 = 1 - (1 - w_0) m^2$

sim_trimodal <- sim_latentG(n = 2000, shape = "trimodal", seed = 1)
plot(sim_trimodal, show_normal = TRUE)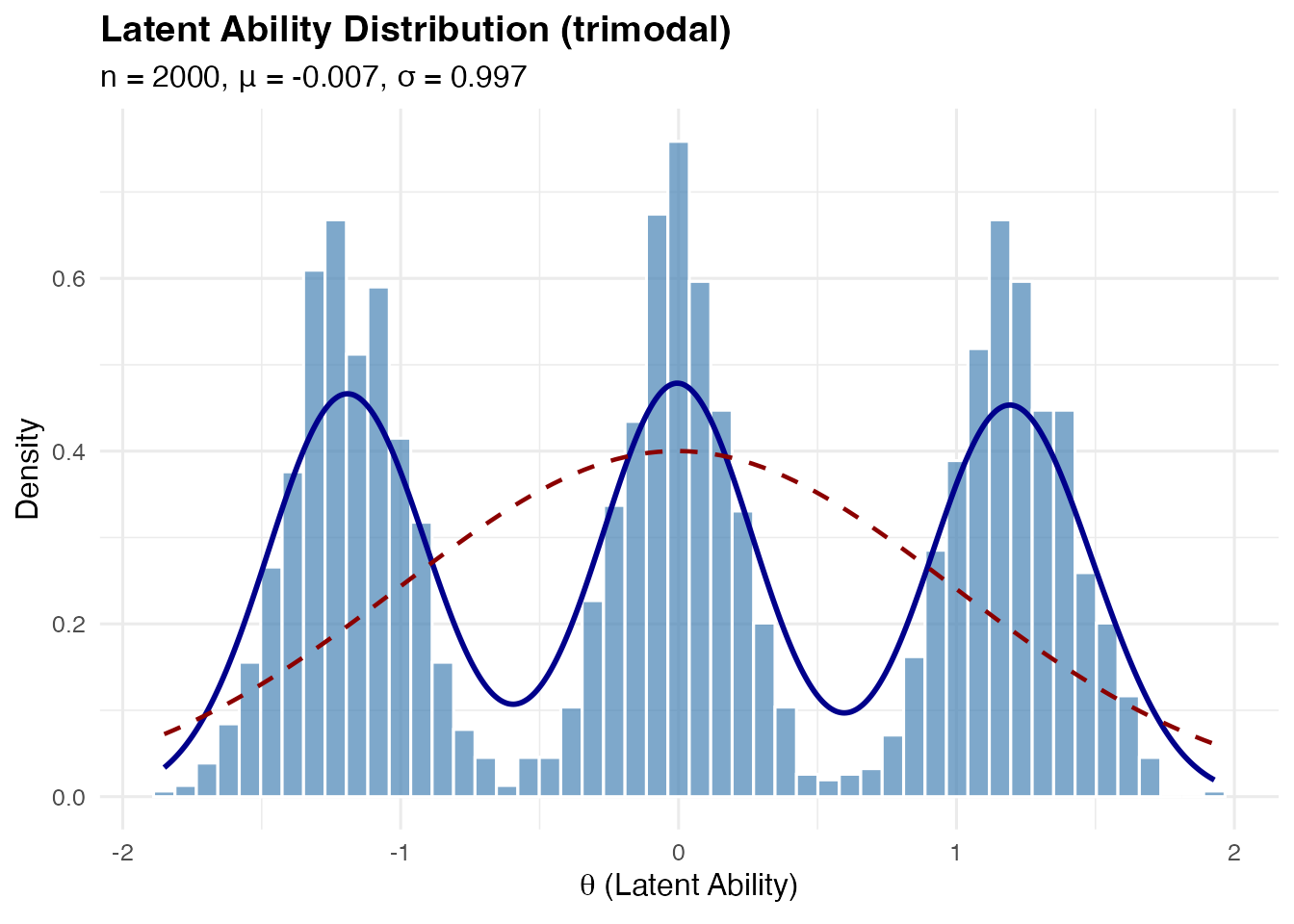

Customizing:

# Stronger central peak
sim_trimodal_central <- sim_latentG(
  n = 2000,
  shape = "trimodal",
  shape_params = list(
    w0 = 0.5,   # Weight of central component (default: 1/3)
    m = 1.3     # Location of side components (default: 1.2)
  ),
  seed = 1
)
plot(sim_trimodal_central, show_normal = TRUE)

Multimodal (Four Components)

A symmetric four-component mixture with modes at $\{-m_2, -m_1, +m_1, +m_2\}$ .

sim_multi <- sim_latentG(n = 2000, shape = "multimodal", seed = 1)
plot(sim_multi, show_normal = TRUE)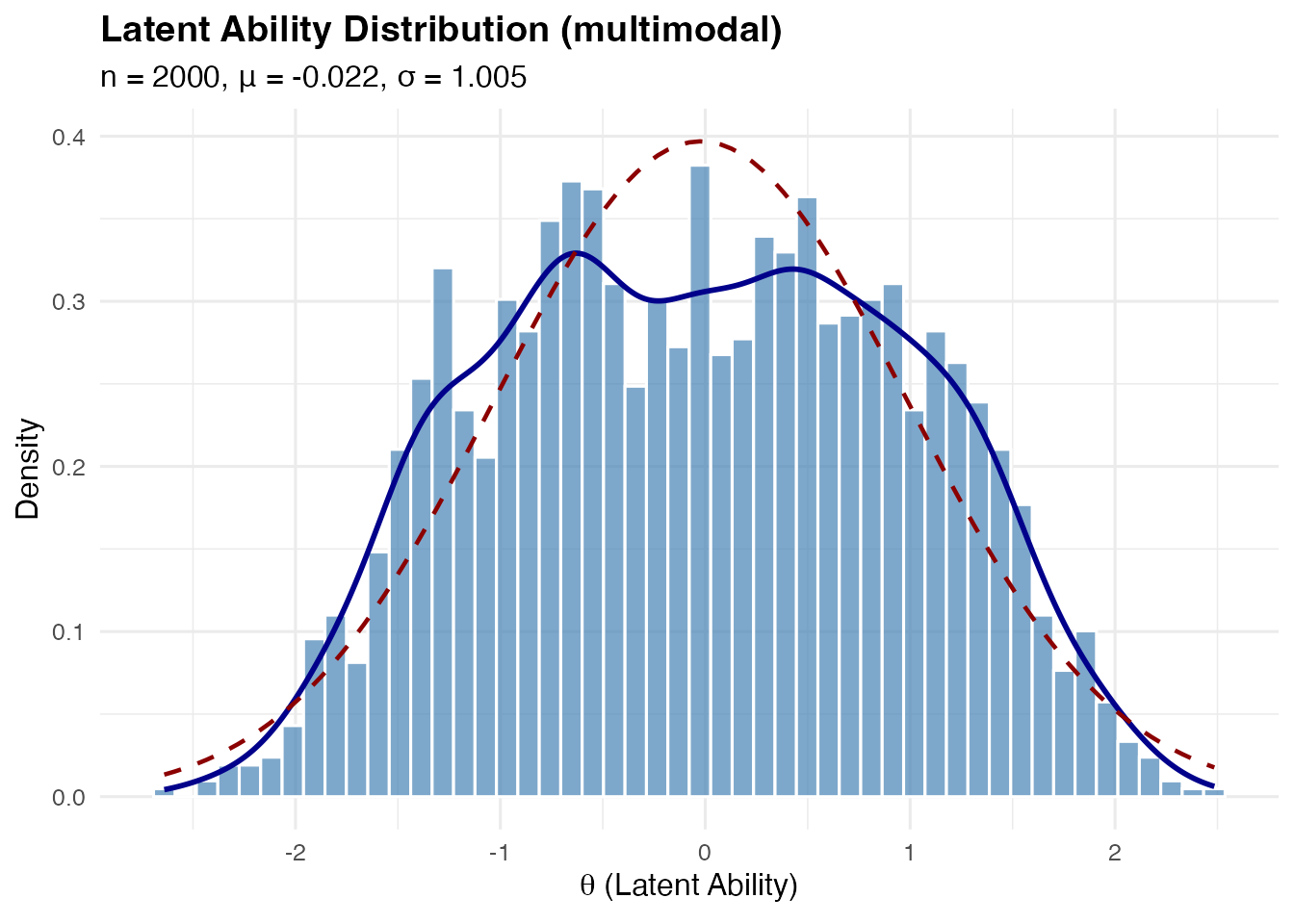

Skewed Distributions

Right-skewed (skew_pos): Based on standardized Gamma distribution:

$z = \frac{\Gamma(k, 1) - k}{\sqrt{k}}$

This has $\mathbb{E}[z] = 0$ and $\text{Var}[z] = 1$ for any $k > 0$ .

sim_skew_pos <- sim_latentG(n = 2000, shape = "skew_pos", seed = 1)
plot(sim_skew_pos, show_normal = TRUE)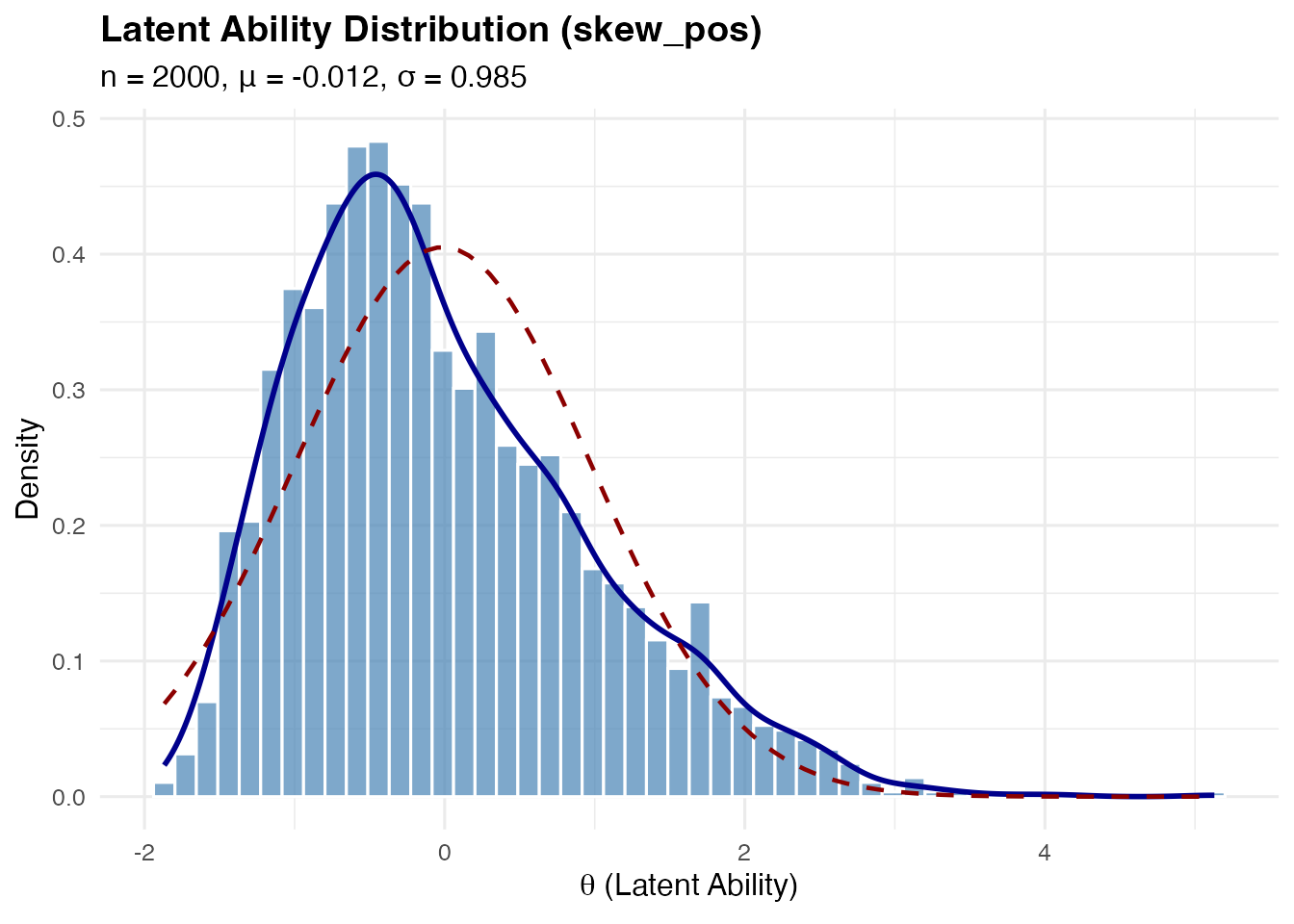

Left-skewed (skew_neg): Simply the negation of the right-skewed distribution.

sim_skew_neg <- sim_latentG(n = 2000, shape = "skew_neg", seed = 1)
plot(sim_skew_neg, show_normal = TRUE)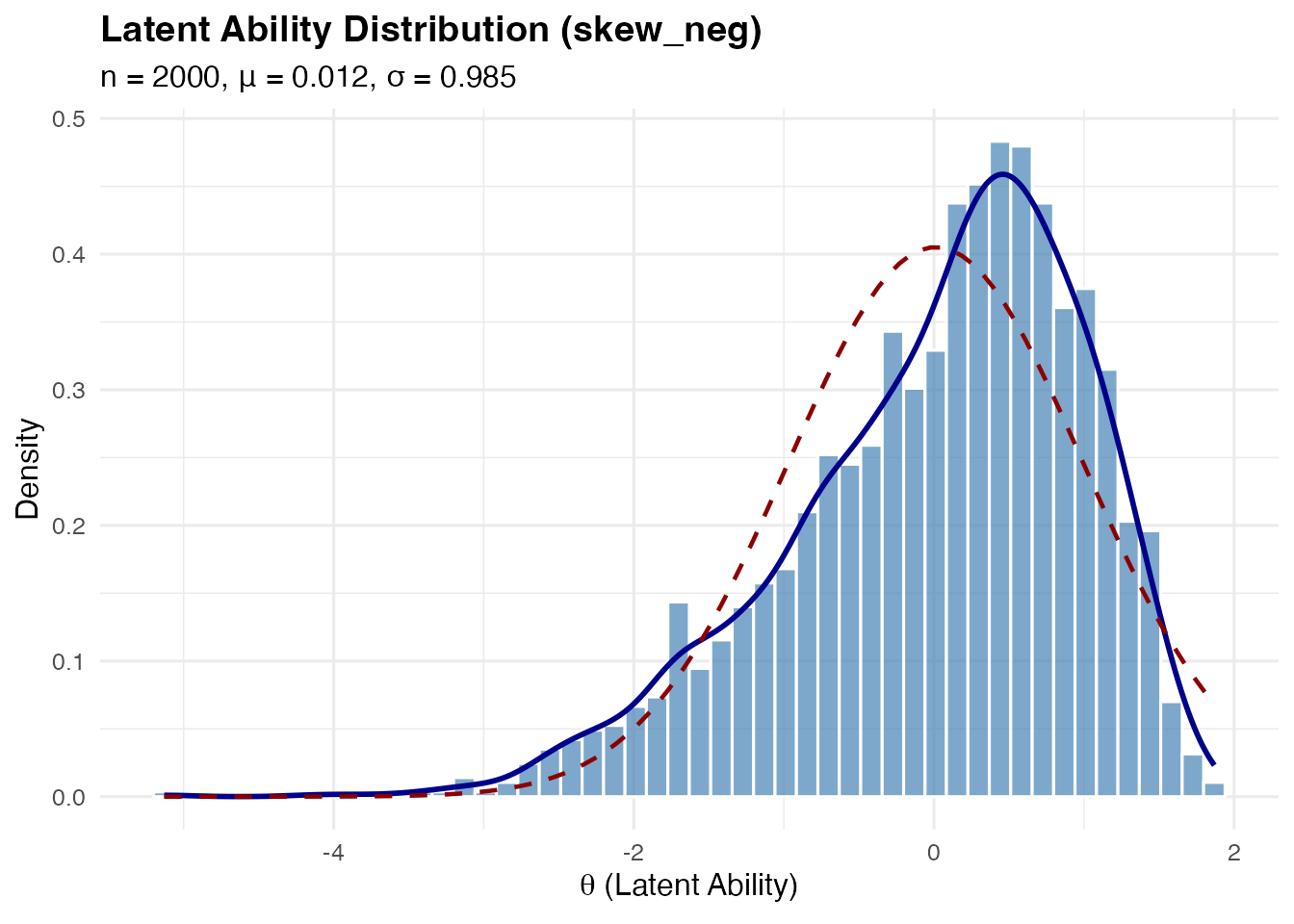

Controlling skewness magnitude:

The k parameter (Gamma shape) controls skewness—smaller values = more skewed:

# More extreme skewness (k = 2)
sim_very_skew <- sim_latentG(
  n = 2000,
  shape = "skew_pos",
  shape_params = list(k = 2),
  seed = 1
)

cat(sprintf("Default k=4 skewness: %.3f\n", sim_skew_pos$sample_moments$skewness))
#> Default k=4 skewness: 0.812
cat(sprintf("k=2 skewness:         %.3f\n", sim_very_skew$sample_moments$skewness))
#> k=2 skewness:         1.244

Heavy-Tailed Distribution

Based on standardized Student-t:

$z = \frac{t_\nu}{\sqrt{\nu / (\nu - 2)}}$

This has $\text{Var}[z] = 1$ for $\nu > 2$ .

sim_heavy <- sim_latentG(n = 2000, shape = "heavy_tail", seed = 1)
plot(sim_heavy, show_normal = TRUE)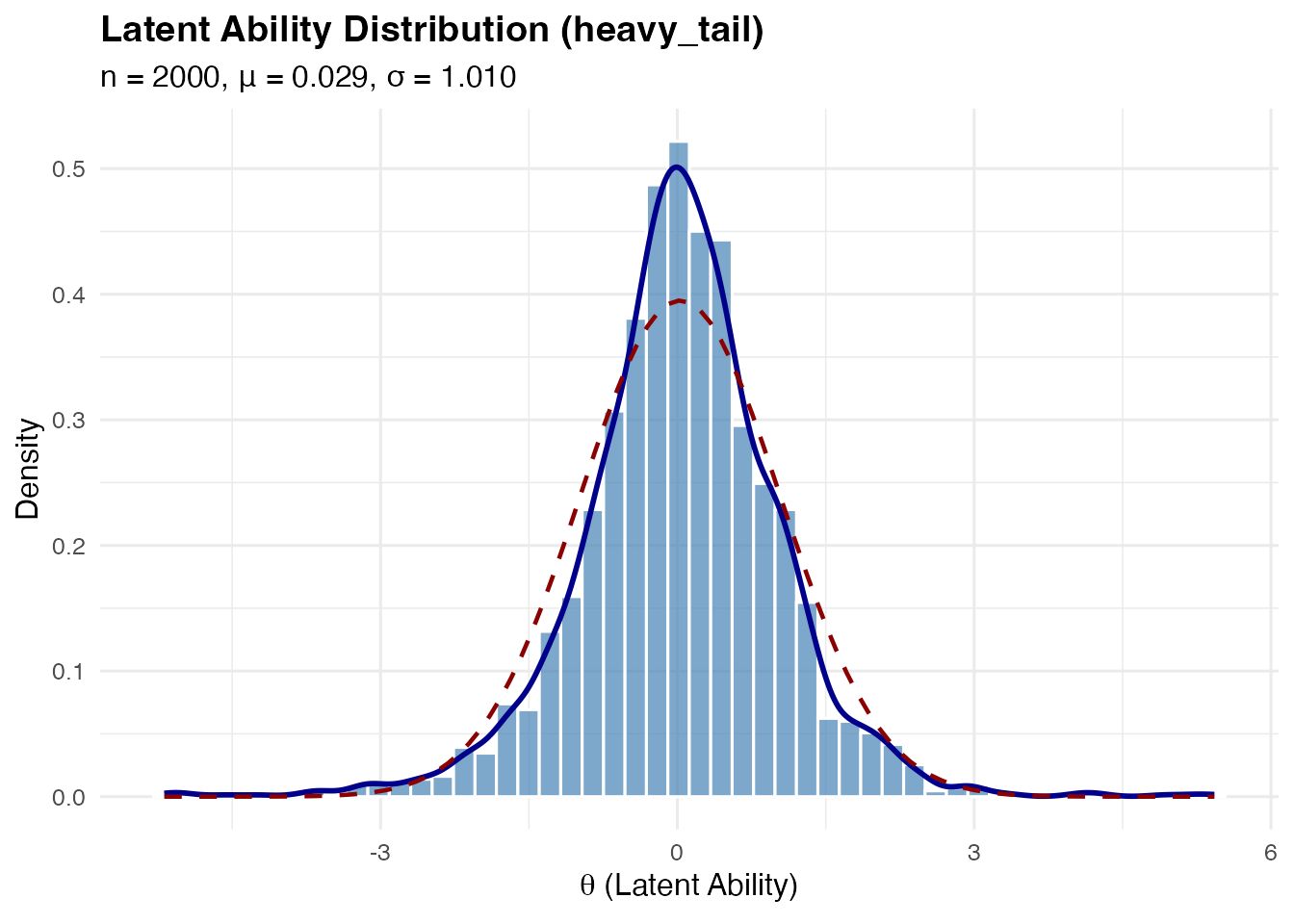

Controlling tail heaviness:

The df parameter (degrees of freedom) controls tail weight—smaller values = heavier tails:

# Very heavy tails (df = 3)
sim_very_heavy <- sim_latentG(
  n = 2000,
  shape = "heavy_tail",
  shape_params = list(df = 3),
  seed = 1
)

cat(sprintf("Default df=5 kurtosis: %.3f\n", sim_heavy$sample_moments$kurtosis))
#> Default df=5 kurtosis: 2.924
cat(sprintf("df=3 kurtosis:         %.3f\n", sim_very_heavy$sample_moments$kurtosis))
#> df=3 kurtosis:         7.956

Light-Tailed (Platykurtic) Distribution

A mixture distribution approximating a platykurtic shape (negative excess kurtosis).

sim_light <- sim_latentG(n = 2000, shape = "light_tail", seed = 1)
plot(sim_light, show_normal = TRUE)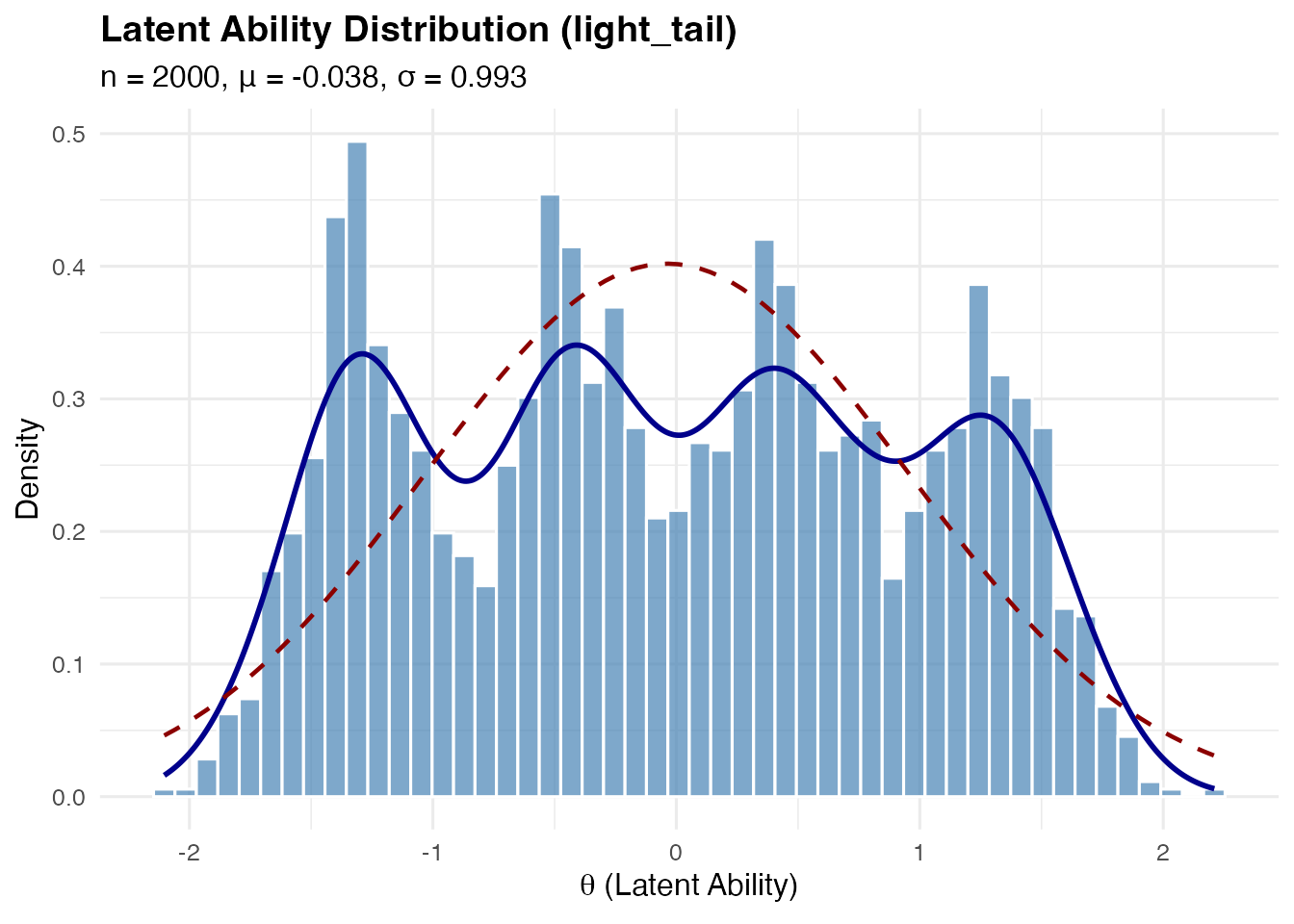

Uniform Distribution

Uniform on $[-\sqrt{3}, +\sqrt{3}]$ , which has mean 0 and variance 1.

sim_uniform <- sim_latentG(n = 2000, shape = "uniform", seed = 1)
plot(sim_uniform, show_normal = TRUE)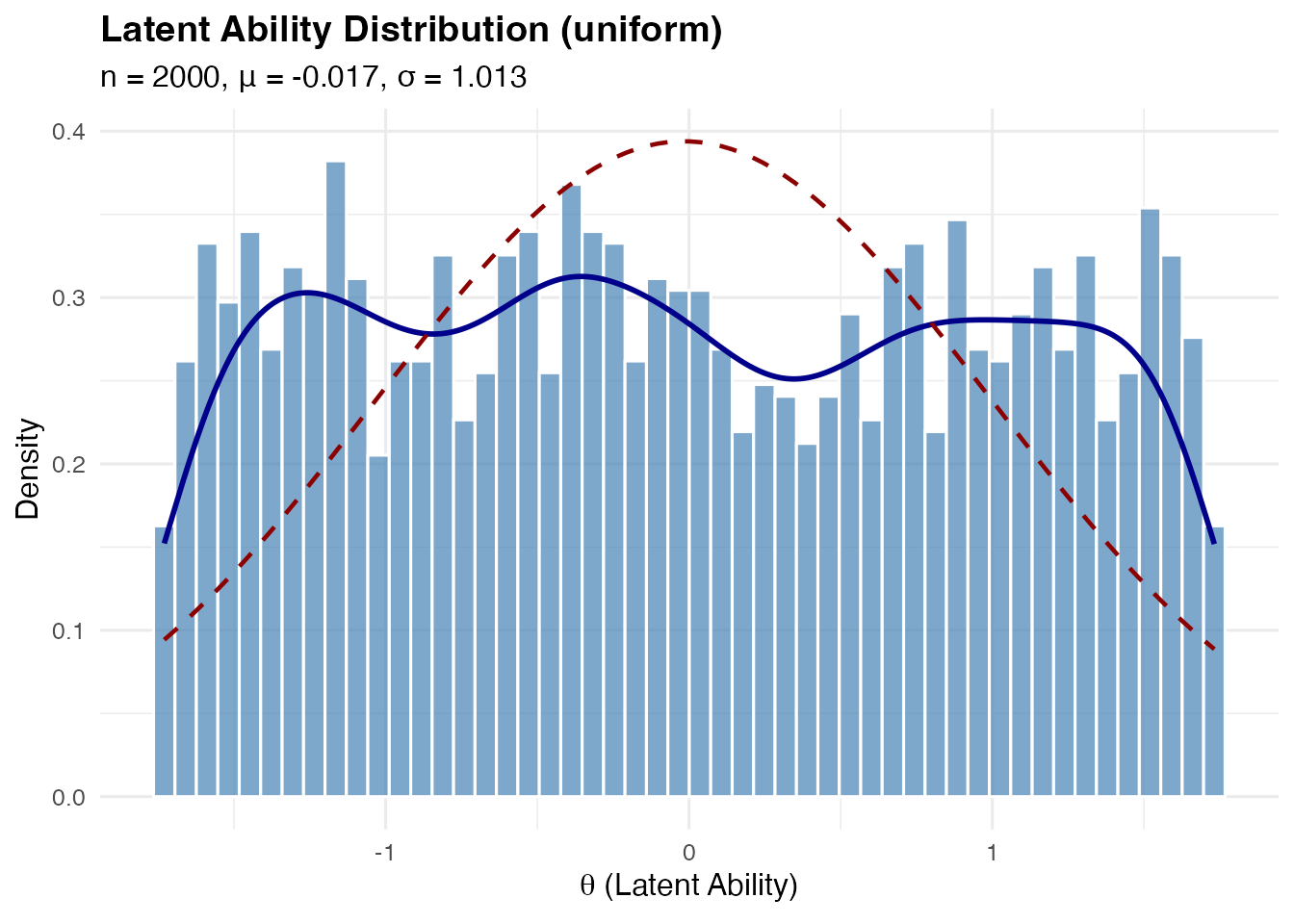

Floor and Ceiling Effects

These represent situations where there’s a concentration of examinees at one end of the ability distribution.

Floor effect: Heavy component near the lower bound (e.g., many low-ability students in a difficult test)

sim_floor <- sim_latentG(n = 2000, shape = "floor", seed = 1)
plot(sim_floor, show_normal = TRUE)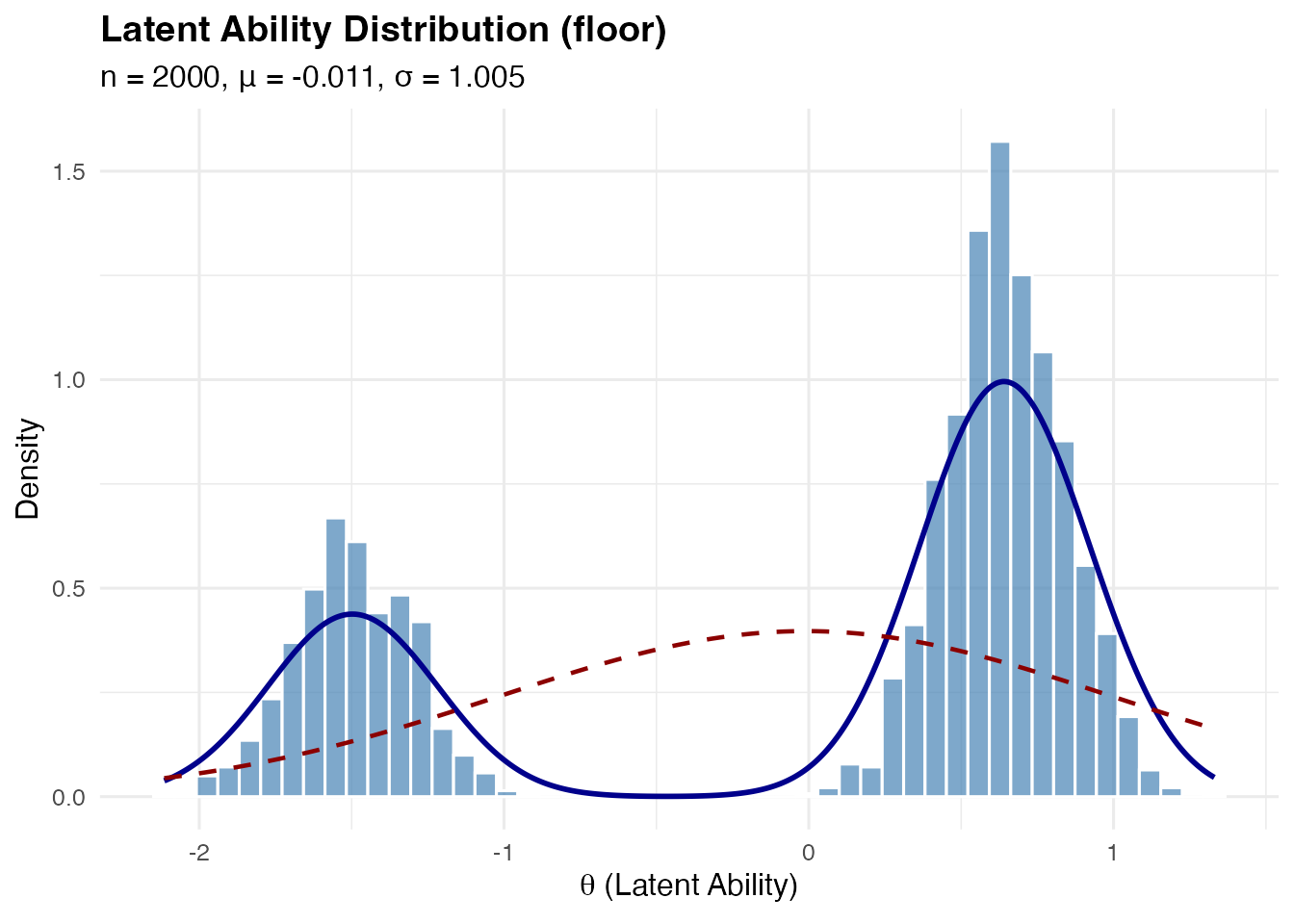

Ceiling effect: Heavy component near the upper bound (e.g., many high-ability students in an easy test)

sim_ceiling <- sim_latentG(n = 2000, shape = "ceiling", seed = 1)
plot(sim_ceiling, show_normal = TRUE)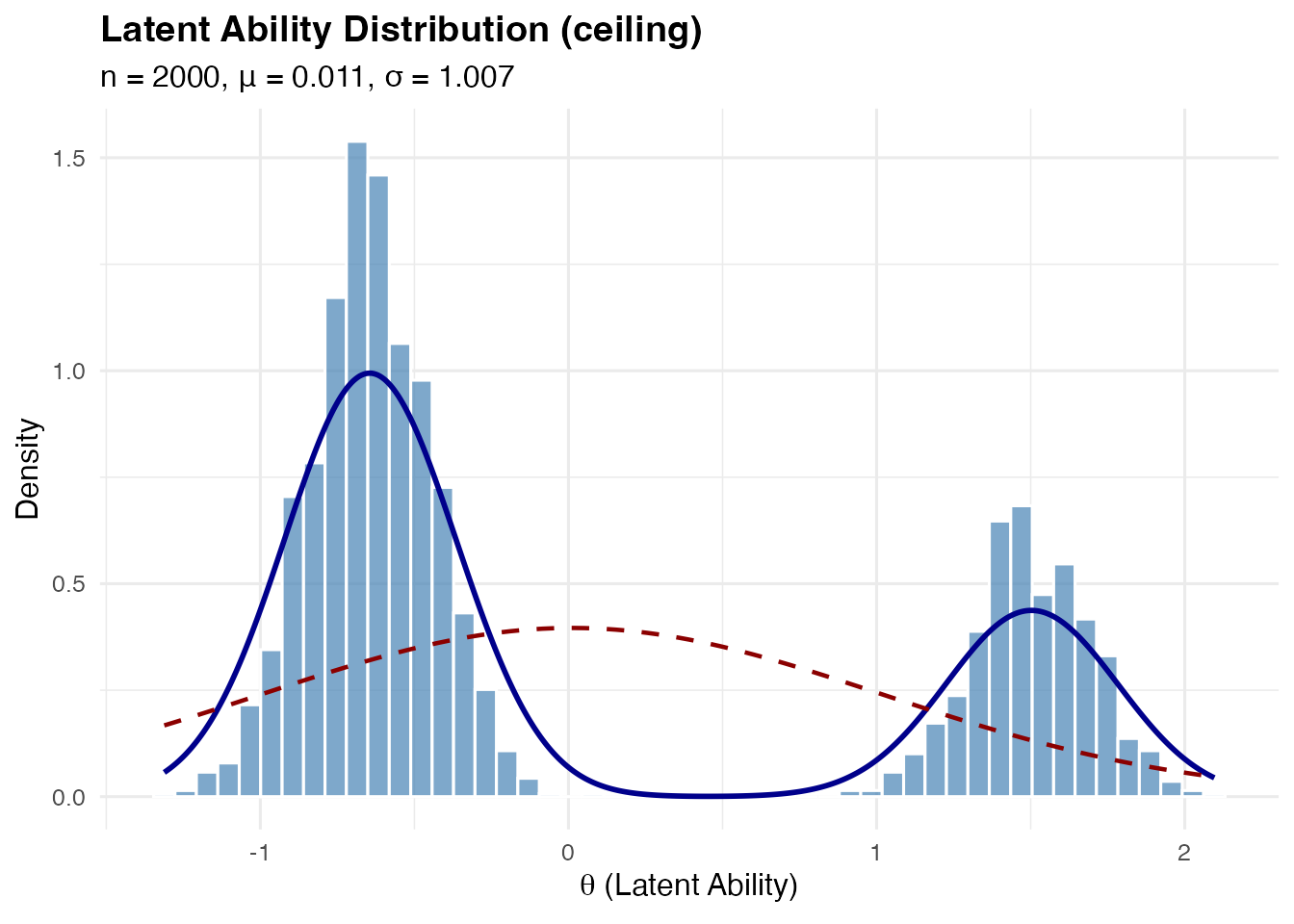

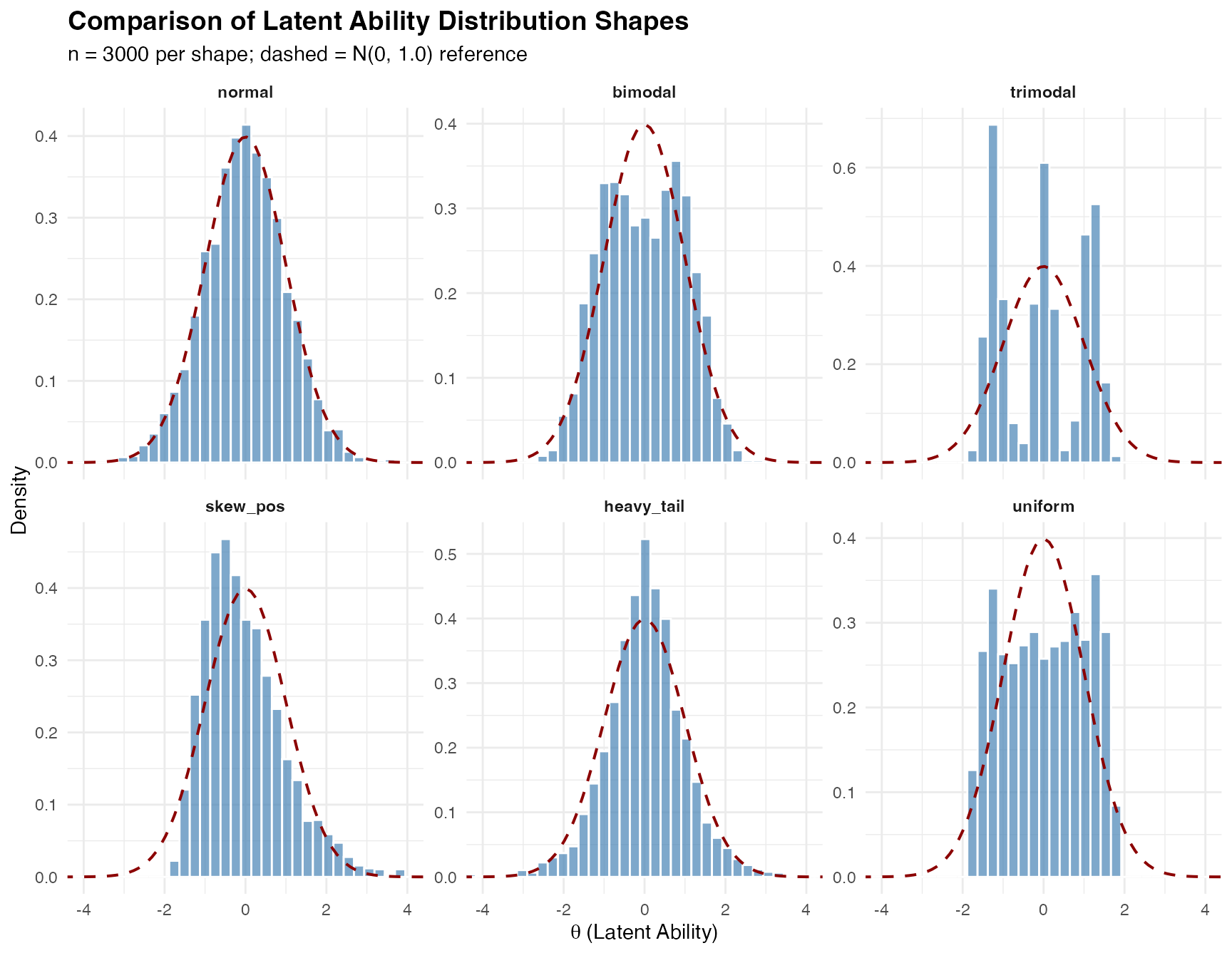
Comparing Multiple Shapes

The compare_shapes() function provides a convenient way to visualize multiple distributions side-by-side:

compare_shapes(
  n = 3000,
  shapes = c("normal", "bimodal", "trimodal", 
             "skew_pos", "heavy_tail", "uniform"),
  sigma = 1,
  seed = 42
)

Custom Mixture Distributions

For maximum flexibility, use shape = "custom" with mixture_spec:

# Define a custom 3-component mixture
sim_custom <- sim_latentG(

n = 2000,
  shape = "custom",
  mixture_spec = list(
    weights = c(0.3, 0.5, 0.2),   # Must sum to 1
    means = c(-1.5, 0, 2),        # Component means
    sds = c(0.5, 0.7, 0.5)        # Component SDs
  ),
  seed = 1
)

plot(sim_custom, show_normal = TRUE)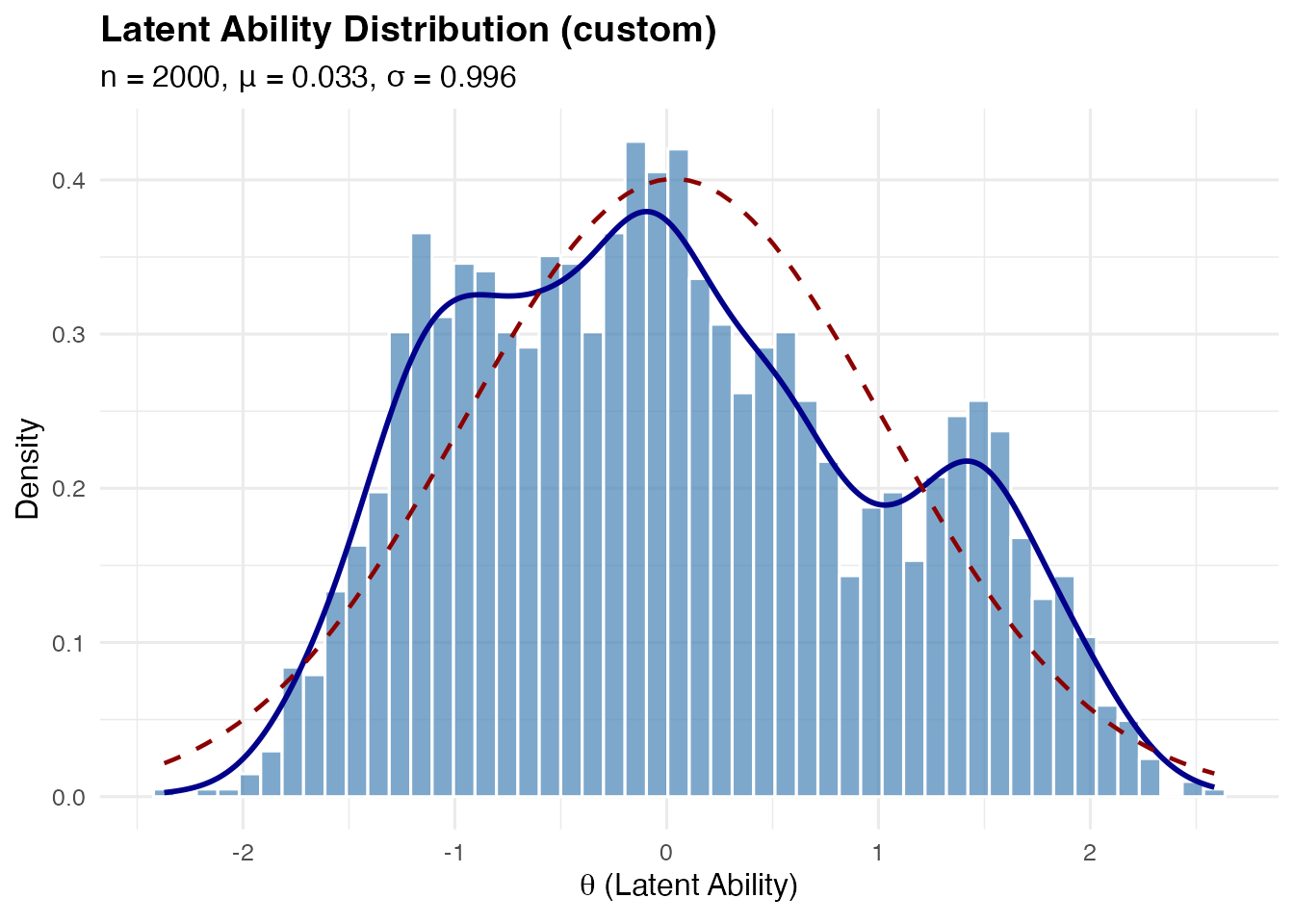

By default, custom mixtures are automatically post-standardized to have mean 0 and variance 1. To disable this:

# Keep raw mixture parameters
sim_raw <- sim_latentG(
  n = 2000,
  shape = "custom",
  mixture_spec = list(
    weights = c(0.5, 0.5),
    means = c(-1, 1),
    sds = c(0.5, 0.5)
  ),
  standardize_custom = FALSE,
  seed = 1
)

Adjusting Location and Scale

The mu and sigma parameters allow you to shift and scale the distribution:

# Generate abilities with mean 100 and SD 15 (like IQ scores)
sim_iq <- sim_latentG(
  n = 1000,
  shape = "normal",
  mu = 100,
  sigma = 15,
  seed = 42
)

summary(sim_iq)
#> Summary: Latent Ability Distribution
#> ====================================
#>   Shape      : normal
#>   n          : 1000
#>   Target     : mu = 100.00, sigma = 15.00
#>   Covariates : No
#> 
#> Sample Statistics:
#>   Mean       : 99.6126
#>   SD         : 15.0378
#>   Median     : 99.8030
#>   Skewness   : -0.0038
#>   Kurtosis   : 0.1286 (excess)
#>   Range      : [49.4239, 152.4296]
#> 
#> Quantiles:
#>     2.5%       5%      25%      50%      75%      95%    97.5% 
#>  69.8816  75.3193  89.8681  99.8030 109.9601 123.0023 128.1655

This works with any shape:

# Bimodal with different scale
sim_bimodal_scaled <- sim_latentG(
  n = 1000,
  shape = "bimodal",
  mu = 0,
  sigma = 1.5,  # Larger spread
  seed = 42
)

cat(sprintf("Sample SD: %.3f (target: 1.5)\n", sd(sim_bimodal_scaled$theta)))
#> Sample SD: 1.481 (target: 1.5)

Adding Covariate Effects

You can incorporate person-level covariates that affect ability:

# Create covariate data
n <- 1000
set.seed(42)
group <- rbinom(n, 1, 0.5)           # Binary group indicator
ses <- rnorm(n)                       # Continuous SES measure

# Generate abilities with covariate effects
sim_cov <- sim_latentG(
  n = n,
  shape = "normal",
  xcov = data.frame(group = group, ses = ses),
  beta = c(0.5, 0.3),  # Group effect = 0.5, SES effect = 0.3
  seed = 42
)

# Verify covariate effects
cat("Mean ability by group:\n")
#> Mean ability by group:
cat(sprintf("  Group 0: %.3f\n", mean(sim_cov$theta[group == 0])))
#>   Group 0: -0.084
cat(sprintf("  Group 1: %.3f\n", mean(sim_cov$theta[group == 1])))
#>   Group 1: 0.519
cat(sprintf("  Difference: %.3f (expected: 0.5)\n", 
            mean(sim_cov$theta[group == 1]) - mean(sim_cov$theta[group == 0])))
#>   Difference: 0.602 (expected: 0.5)

The full model is:

$\theta_p = \mu + X_p^\top \beta + \sigma \cdot z_p$

where $X_p$ is the covariate vector for person $p$ .

Working with the Output Object

The sim_latentG() function returns a latent_G object containing:

sim <- sim_latentG(n = 100, shape = "bimodal", seed = 1)

# Available components
names(sim)
#> [1] "theta"          "mu"             "sigma"          "eta_cov"       
#> [5] "shape"          "shape_params"   "n"              "sample_moments"
#> [9] "z"

# The theta vector
head(sim$theta)
#> [1] -0.5611365  0.4327842 -0.5953282 -1.4776179  1.6598142  0.3882399

# The standardized z values (before scaling)
head(sim$z)
#> [1] -0.5611365  0.4327842 -0.5953282 -1.4776179  1.6598142  0.3882399

# Sample moments
sim$sample_moments
#> $mean
#> [1] 0.005452304
#> 
#> $sd
#> [1] 0.9591602
#> 
#> $skewness
#> [1] -0.1115873
#> 
#> $kurtosis
#> [1] -1.109185

Extracting theta for Other Uses

# Get theta as a numeric vector
theta_vec <- sim$theta

# Use in your own analysis
mean(theta_vec)
#> [1] 0.005452304

Connection to IRT Framework

In the Rasch/2PL model, the latent distribution $G$ affects key quantities:

Marginal Reliability

$\bar{w} = \frac{\sigma^2_\theta}{\sigma^2_\theta + \text{MSEM}}$

where MSEM is the mean squared error of measurement.

Expected Test Information

$\bar{\mathcal{J}} = \mathbb{E}_G[\mathcal{J}(\theta)]$

Different latent shapes produce different expected information profiles, even with identical item parameters.

Identifiability

For model identification in the Rasch model, we typically fix either:

$\mathbb{E}[\theta] = 0$ (location constraint), or
$\sum_i \beta_i = 0$ (item constraint)

The sim_latentG() function generates abilities with mean 0 by default, supporting the first identification approach.

Using sim_latentG with eqc_calibrate

When using sim_latentG() as part of reliability-targeted simulation, specify the same parameters in eqc_calibrate():

# Calibrate for a bimodal population
eqc_result <- eqc_calibrate(
  target_rho = 0.80,
  n_items = 25,
  model = "rasch",
  latent_shape = "bimodal",
  latent_params = list(delta = 0.8),
  seed = 42
)

# Generate response data with the same distribution
sim_data <- simulate_response_data(
  eqc_result = eqc_result,
  n_persons = 1000,
  latent_shape = "bimodal",
  latent_params = list(delta = 0.8),
  seed = 123
)

Summary of Shape Parameters

Shape	Parameter	Default	Range	Description
`bimodal`	`delta`	0.8	(0, 1)	Mode separation
`trimodal`	`w0`	1/3	(0, 1)	Weight of central component
	`m`	1.2	> 0	Location of side modes
`multimodal`	`m1`	0.5	> 0	Inner mode locations
	`m2`	1.3	> 0	Outer mode locations
	`w_inner`	0.30	(0, 0.5)	Weight of inner components
`skew_pos/neg`	`k`	4	> 0	Gamma shape (smaller = more skewed)
`heavy_tail`	`df`	5	> 2	Degrees of freedom (smaller = heavier)
`floor`	`w_floor`	0.3	(0, 1)	Weight at floor
	`m_floor`	-1.5	< 0	Floor location
`ceiling`	`w_ceil`	0.3	(0, 1)	Weight at ceiling
	`m_ceil`	1.5	> 0	Ceiling location

Practical Recommendations

Choosing a Shape

Research Question	Recommended Shape
Standard simulation	`normal`
Heterogeneous population	`bimodal`
Mixed ability levels	`trimodal` or `multimodal`
Selective samples	`skew_pos` or `skew_neg`
Robust estimation	`heavy_tail`
Easy/difficult tests	`ceiling` / `floor`
Sensitivity analysis	Compare multiple shapes

Sample Size Considerations

For stable Monte Carlo estimates:

M = 10,000 or more for eqc_calibrate() quadrature
n = 500–2000 per replication for simulation studies
Increase n for heavy-tailed or highly multimodal shapes

Reproducibility

Always set a seed for reproducible results:

sim1 <- sim_latentG(n = 100, shape = "normal", seed = 42)
sim2 <- sim_latentG(n = 100, shape = "normal", seed = 42)
identical(sim1$theta, sim2$theta)  # TRUE
#> [1] TRUE