Skip to contents

Generating Realistic Item Parameters

Source: vignettes/item_parameters.Rmd
item_parameters.Rmd

Overview

The sim_item_params() function generates item parameters (difficulty β\beta and discrimination λ\lambda) for IRT simulation studies. It is designed with four key principles:

  1. Realistic difficulties: Integration with the Item Response Warehouse (IRW) for empirically-grounded difficulty distributions
  2. Correlated parameters: Support for the empirically-observed negative correlation between difficulty and discrimination
  3. Marginal preservation: The copula method preserves exact marginal distributions
  4. Reliability targeting: A scale factor enables subsequent calibration for target reliability

This vignette covers:

  • Sources for difficulty generation
  • Methods for discrimination generation
  • The difficulty-discrimination correlation
  • Generating multiple test forms
  • Integration with reliability-targeted calibration

The Difficulty-Discrimination Correlation

A critical finding from psychometric research is that item difficulty and discrimination are negatively correlated in real assessments (Sweeney et al., 2022). That is:

  • Easy items (β\beta low) tend to have higher discrimination (λ\lambda high)
  • Difficult items (β\beta high) tend to have lower discrimination (λ\lambda low)

This correlation, typically around ρ≈−0.3\rho \approx -0.3, has important implications:

  • Ignoring it produces unrealistic simulation data
  • Standard independent generation misses this structural feature
  • The correlation affects test information functions

sim_item_params() handles this by default using the copula method with rho = -0.3.

Basic Usage

Rasch Model

For the Rasch model, all discriminations are set to 1:

# Generate 25 Rasch items with IRW difficulties
items_rasch <- sim_item_params(
  n_items = 25,
  model = "rasch",
  source = "irw",
  seed = 42
)

print(items_rasch)
#> Item Parameters Object
#> ======================
#>   Model          : RASCH
#>   Source         : irw
#>   Items per form : 25
#>   Number of forms: 1
#>   Scale factor   : 1.000
#>   Centered       : Yes
#> 
#> Difficulty (beta):
#>   Mean: -0.0000, SD: 0.7992, Range: [-1.484, 1.469]

2PL Model

For the 2PL model, both difficulties and discriminations are generated:

# Generate 30 2PL items with correlated parameters
items_2pl <- sim_item_params(
  n_items = 30,
  model = "2pl",
  source = "irw",
  method = "copula",
  seed = 42
)

print(items_2pl)
#> Item Parameters Object
#> ======================
#>   Model          : 2PL
#>   Source         : irw
#>   Method         : copula
#>   Items per form : 30
#>   Number of forms: 1
#>   Scale factor   : 1.000
#>   Centered       : Yes
#> 
#> Difficulty (beta):
#>   Mean: -0.0000, SD: 0.8357, Range: [-1.607, 1.463]
#> 
#> Discrimination (lambda, scaled):
#>   Mean: 1.0865, SD: 0.4031, Range: [0.590, 2.107]
#> 
#> Correlation (beta, log-lambda):
#>   Target (rho): -0.300
#>   Achieved Pearson : -0.330
#>   Achieved Spearman: -0.466

Notice the achieved correlation between β\beta and log(λ)\log(\lambda) is close to the target of -0.3.

Sources for Difficulty Generation

sim_item_params() supports four sources for generating item difficulties:

1. IRW (Item Response Warehouse)

The recommended source for realistic simulations. IRW provides empirically-grounded difficulty distributions based on thousands of real assessment items.

items_irw <- sim_item_params(
  n_items = 25,
  model = "rasch",
  source = "irw",
  seed = 42
)

# Examine difficulty distribution
summary(items_irw$data$beta)
#>     Min.  1st Qu.   Median     Mean  3rd Qu.     Max. 
#> -1.48424 -0.54581 -0.08185  0.00000  0.48541  1.46931

Requirements: The irw package must be installed:

# Install IRW package from GitHub
devtools::install_github("itemresponsewarehouse/irw")

2. Parametric

Generate difficulties from a parametric distribution:

# Normal distribution
items_normal <- sim_item_params(
  n_items = 25,
  model = "rasch",
  source = "parametric",
  difficulty_params = list(
    mu = 0,
    sigma = 1,
    distribution = "normal"
  ),
  seed = 42
)

# Uniform distribution
items_uniform <- sim_item_params(
  n_items = 25,
  model = "rasch",
  source = "parametric",
  difficulty_params = list(
    mu = 0,
    sigma = 1,
    distribution = "uniform"
  ),
  seed = 42
)

3. Hierarchical

Joint bivariate normal generation following Glas & van der Linden (2003). Both log(λ)\log(\lambda) and β\beta are drawn from a multivariate normal:

(log(λi)βi)∼N((μλμβ),(τλ2ρτλτβρτλτβτβ2))\begin{pmatrix} \log(\lambda_i) \\ \beta_i \end{pmatrix} \sim N\left( \begin{pmatrix} \mu_\lambda \\ \mu_\beta \end{pmatrix}, \begin{pmatrix} \tau_\lambda^2 & \rho \tau_\lambda \tau_\beta \\ \rho \tau_\lambda \tau_\beta & \tau_\beta^2 \end{pmatrix} \right)

items_hier <- sim_item_params(
  n_items = 25,
  model = "2pl",
  source = "hierarchical",
  hierarchical_params = list(
    mu = c(0, 0),      # Means: (log-lambda, beta)
    tau = c(0.25, 1),  # SDs
    rho = -0.3         # Correlation
  ),
  seed = 42
)

print(items_hier)
#> Item Parameters Object
#> ======================
#>   Model          : 2PL
#>   Source         : hierarchical
#>   Items per form : 25
#>   Number of forms: 1
#>   Scale factor   : 1.000
#>   Centered       : Yes
#> 
#> Difficulty (beta):
#>   Mean: -0.0000, SD: 1.3077, Range: [-2.863, 2.109]
#> 
#> Discrimination (lambda, scaled):
#>   Mean: 1.0776, SD: 0.2710, Range: [0.720, 1.812]
#> 
#> Correlation (beta, log-lambda):
#>   Target (rho): -0.300
#>   Achieved Pearson : -0.345
#>   Achieved Spearman: -0.375

4. Custom

Supply your own parameters directly:

# Custom difficulties and discriminations
items_custom <- sim_item_params(
  n_items = 10,
  model = "2pl",
  source = "custom",
  custom_params = list(
    beta = seq(-2, 2, length.out = 10),
    lambda = rep(1.2, 10)
  ),
  seed = 42
)
#> Warning in cor(df$beta, log(df$lambda_unscaled)): the standard deviation is
#> zero
#> Warning in cor(df$beta, log(df$lambda_unscaled), method = "spearman"): the
#> standard deviation is zero
#> Warning in cor(data$beta, log(data$lambda_unscaled)): the standard deviation is
#> zero
#> Warning in cor(data$beta, log(data$lambda_unscaled), method = "spearman"): the
#> standard deviation is zero

items_custom$data
#>    form_id item_id       beta lambda lambda_unscaled
#> 1        1       1 -2.0000000    1.2             1.2
#> 2        1       2 -1.5555556    1.2             1.2
#> 3        1       3 -1.1111111    1.2             1.2
#> 4        1       4 -0.6666667    1.2             1.2
#> 5        1       5 -0.2222222    1.2             1.2
#> 6        1       6  0.2222222    1.2             1.2
#> 7        1       7  0.6666667    1.2             1.2
#> 8        1       8  1.1111111    1.2             1.2
#> 9        1       9  1.5555556    1.2             1.2
#> 10       1      10  2.0000000    1.2             1.2

You can also provide functions that generate parameters:

items_custom_fn <- sim_item_params(
  n_items = 20,
  model = "2pl",
  source = "custom",
  custom_params = list(
    beta = function(n) rnorm(n, 0, 1.5),
    lambda = function(n) rlnorm(n, 0, 0.3)
  ),
  seed = 42
)

Methods for Discrimination Generation

When using source = "irw" or source = "parametric" with model = "2pl", you need to specify how discriminations are generated. Three methods are available:

The Gaussian copula method preserves exact marginal distributions while achieving the target correlation:

Algorithm:

  1. Transform β\beta to uniform via empirical CDF: u=rank(β)/(n+1)u = \text{rank}(\beta) / (n+1)
  2. Transform to normal: zβ=Φ−1(u)z_\beta = \Phi^{-1}(u)
  3. Generate correlated normal: zλ=ρ⋅zβ+1−ρ2⋅zindepz_\lambda = \rho \cdot z_\beta + \sqrt{1-\rho^2} \cdot z_{\text{indep}}
  4. Transform to uniform: v=Φ(zλ)v = \Phi(z_\lambda)
  5. Transform to log-normal: λ=exp(μ+σ⋅Φ−1(v))\lambda = \exp(\mu + \sigma \cdot \Phi^{-1}(v)) 
items_copula <- sim_item_params(
  n_items = 100,
  model = "2pl",
  source = "irw",
  method = "copula",
  discrimination_params = list(
    mu_log = 0,       # Mean of log(lambda)
    sigma_log = 0.3,  # SD of log(lambda)
    rho = -0.3        # Target correlation
  ),
  seed = 42
)

# Check achieved correlation
cat(sprintf("Target rho: -0.30\n"))
#> Target rho: -0.30
cat(sprintf("Achieved Spearman: %.3f\n", 
            items_copula$achieved$overall$cor_spearman_pooled))
#> Achieved Spearman: -0.191

Why Copula is Recommended:

  • Preserves the exact IRW difficulty distribution
  • Guarantees log-normal marginal for discriminations
  • Achieves target Spearman correlation (robust to non-normality)
  • Works well with any difficulty distribution shape

2. Conditional Method

Uses conditional normal regression:

log(λi)∣βi∼N(μlog+ρ⋅σlog⋅zβi,σlog1−ρ2)\log(\lambda_i) \mid \beta_i \sim N\left(\mu_{\log} + \rho \cdot \sigma_{\log} \cdot z_{\beta_i}, \; \sigma_{\log}\sqrt{1-\rho^2}\right)

items_cond <- sim_item_params(
  n_items = 100,
  model = "2pl",
  source = "irw",
  method = "conditional",
  discrimination_params = list(rho = -0.3),
  seed = 42
)

cat(sprintf("Achieved Pearson:  %.3f\n", 
            items_cond$achieved$overall$cor_pearson_pooled))
#> Achieved Pearson:  -0.248
cat(sprintf("Achieved Spearman: %.3f\n", 
            items_cond$achieved$overall$cor_spearman_pooled))
#> Achieved Spearman: -0.207

Note: The conditional method assumes linear relationships and normal errors. When IRW difficulties are non-normal, achieved correlations may differ from targets.

3. Independent Method

Generates discriminations independently of difficulties (no correlation):

items_indep <- sim_item_params(
  n_items = 100,
  model = "2pl",
  source = "irw",
  method = "independent",
  seed = 42
)

cat(sprintf("Achieved correlation: %.3f (expected: ~0)\n",
            items_indep$achieved$overall$cor_spearman_pooled))
#> Achieved correlation: 0.051 (expected: ~0)

Customizing Discrimination Parameters

The discrimination_params list controls the log-normal distribution of discriminations:

# Higher average discrimination
items_high_disc <- sim_item_params(
  n_items = 30,
  model = "2pl",
  source = "irw",
  method = "copula",
  discrimination_params = list(
    mu_log = 0.3,     # E[lambda] ≈ exp(0.3) ≈ 1.35
    sigma_log = 0.25, # Less variation
    rho = -0.3
  ),
  seed = 42
)

cat(sprintf("Mean lambda: %.3f\n", mean(items_high_disc$data$lambda)))
#> Mean lambda: 1.435
cat(sprintf("SD lambda:   %.3f\n", sd(items_high_disc$data$lambda)))
#> SD lambda:   0.435

Understanding the Parameters

Parameter Default Description
mu_log 0 Mean of log(λ)\log(\lambda). 𝔼[λ]≈exp(μlog+σlog2/2)\mathbb{E}[\lambda] \approx \exp(\mu_{\log} + \sigma_{\log}^2/2)
sigma_log 0.3 SD of log(λ)\log(\lambda). Controls heterogeneity across items
rho -0.3 Target correlation between β\beta and log(λ)\log(\lambda)

Generating Multiple Test Forms

Generate multiple parallel forms with independent item samples:

items_5forms <- sim_item_params(
  n_items = 20,
  model = "2pl",
  source = "irw",
  method = "copula",
  n_forms = 5,
  seed = 42
)

# Check structure
cat(sprintf("Total items: %d\n", nrow(items_5forms$data)))
#> Total items: 100
cat(sprintf("Items per form: %d\n", items_5forms$n_items))
#> Items per form: 20
cat(sprintf("Number of forms: %d\n", items_5forms$n_forms))
#> Number of forms: 5

# View first few rows
head(items_5forms$data, 10)
#>    form_id item_id        beta    lambda lambda_unscaled
#> 1        1       1 -0.31979479 0.9134159       0.9134159
#> 2        1       2 -0.13448739 1.1691256       1.1691256
#> 3        1       3  1.21101694 0.6461936       0.6461936
#> 4        1       4  0.07285940 1.2932730       1.2932730
#> 5        1       5 -1.41375360 1.2920870       1.2920870
#> 6        1       6  0.49929409 0.9477748       0.9477748
#> 7        1       7 -0.86741035 1.0869113       1.0869113
#> 8        1       8  0.71169376 0.9945658       0.9945658
#> 9        1       9  0.58379081 0.7129531       0.7129531
#> 10       1      10 -0.04531184 1.0322409       1.0322409

Per-Form Statistics 

# Access per-form statistics
for (f in 1:3) {
  stats <- items_5forms$achieved$by_form[[f]]
  cat(sprintf("Form %d: beta_mean=%.3f, lambda_mean=%.3f, cor=%.3f\n",
              f, stats$beta_mean, stats$lambda_mean, stats$cor_spearman))
}
#> Form 1: beta_mean=0.000, lambda_mean=1.027, cor=-0.540
#> Form 2: beta_mean=0.000, lambda_mean=1.152, cor=-0.202
#> Form 3: beta_mean=0.000, lambda_mean=1.109, cor=-0.320

The Scale Parameter

The scale parameter is crucial for reliability-targeted simulation. It multiplies all discriminations by a constant factor:

λi*=c⋅λi,0\lambda_i^* = c \cdot \lambda_{i,0}

where λi,0\lambda_{i,0} is the baseline discrimination and cc is the scale factor.

# Baseline (scale = 1)
items_base <- sim_item_params(
  n_items = 25,
  model = "2pl",
  source = "irw",
  scale = 1,
  seed = 42
)

# Scaled up (scale = 1.5)
items_scaled <- sim_item_params(
  n_items = 25,
  model = "2pl",
  source = "irw",
  scale = 1.5,
  seed = 42
)

cat(sprintf("Baseline mean lambda: %.3f\n", mean(items_base$data$lambda)))
#> Baseline mean lambda: 1.026
cat(sprintf("Scaled mean lambda:   %.3f\n", mean(items_scaled$data$lambda)))
#> Scaled mean lambda:   1.539
cat(sprintf("Ratio: %.2f\n", 
            mean(items_scaled$data$lambda) / mean(items_base$data$lambda)))
#> Ratio: 1.50

Unscaled Lambda

The output always includes lambda_unscaled for reference:

# Both are stored
head(items_scaled$data[, c("lambda", "lambda_unscaled")])
#>     lambda lambda_unscaled
#> 1 1.556978       1.0379855
#> 2 1.496971       0.9979810
#> 3 1.501281       1.0008540
#> 4 1.152807       0.7685377
#> 5 1.852231       1.2348209
#> 6 1.592726       1.0618176

# Verify relationship
all.equal(
  items_scaled$data$lambda,
  items_scaled$data$lambda_unscaled * items_scaled$scale
)
#> [1] TRUE

Centering Difficulties

By default, difficulties are centered to sum to zero (for model identification):

# Default: centered
items_centered <- sim_item_params(
  n_items = 25,
  model = "rasch",
  source = "irw",
  center_difficulties = TRUE,
  seed = 42
)

# Uncentered
items_uncentered <- sim_item_params(
  n_items = 25,
  model = "rasch",
  source = "irw",
  center_difficulties = FALSE,
  seed = 42
)

cat(sprintf("Centered mean:   %.6f\n", mean(items_centered$data$beta)))
#> Centered mean:   -0.000000
cat(sprintf("Uncentered mean: %.6f\n", mean(items_uncentered$data$beta)))
#> Uncentered mean: 0.018108

Visualization

The plot() method provides diagnostic visualizations:

items_viz <- sim_item_params(
  n_items = 50,
  model = "2pl",
  source = "irw",
  method = "copula",
  seed = 42
)

# Scatter plot with regression line
plot(items_viz, type = "scatter")
#> `geom_smooth()` using formula = 'y ~ x'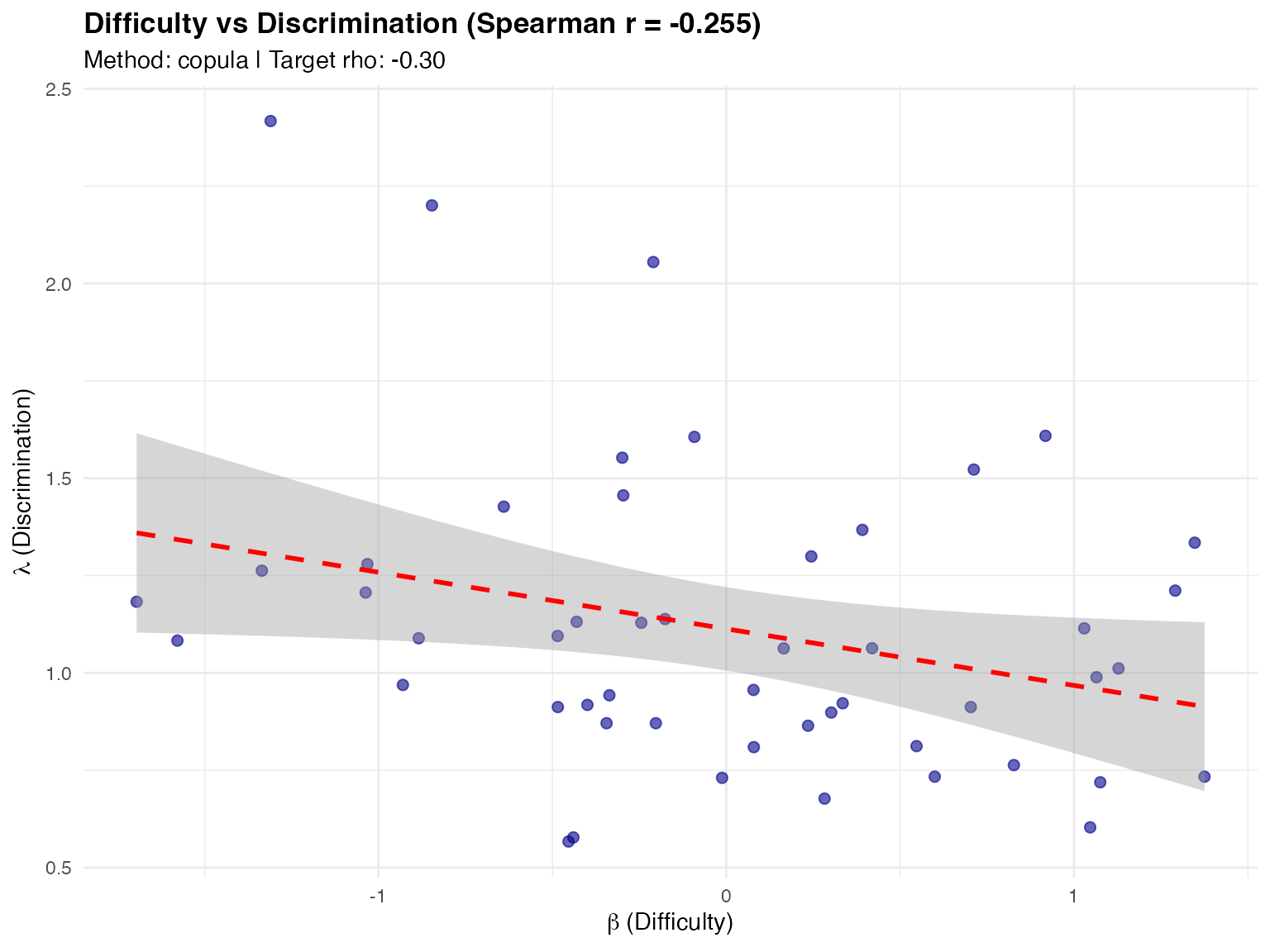

# Density plots
plot(items_viz, type = "density")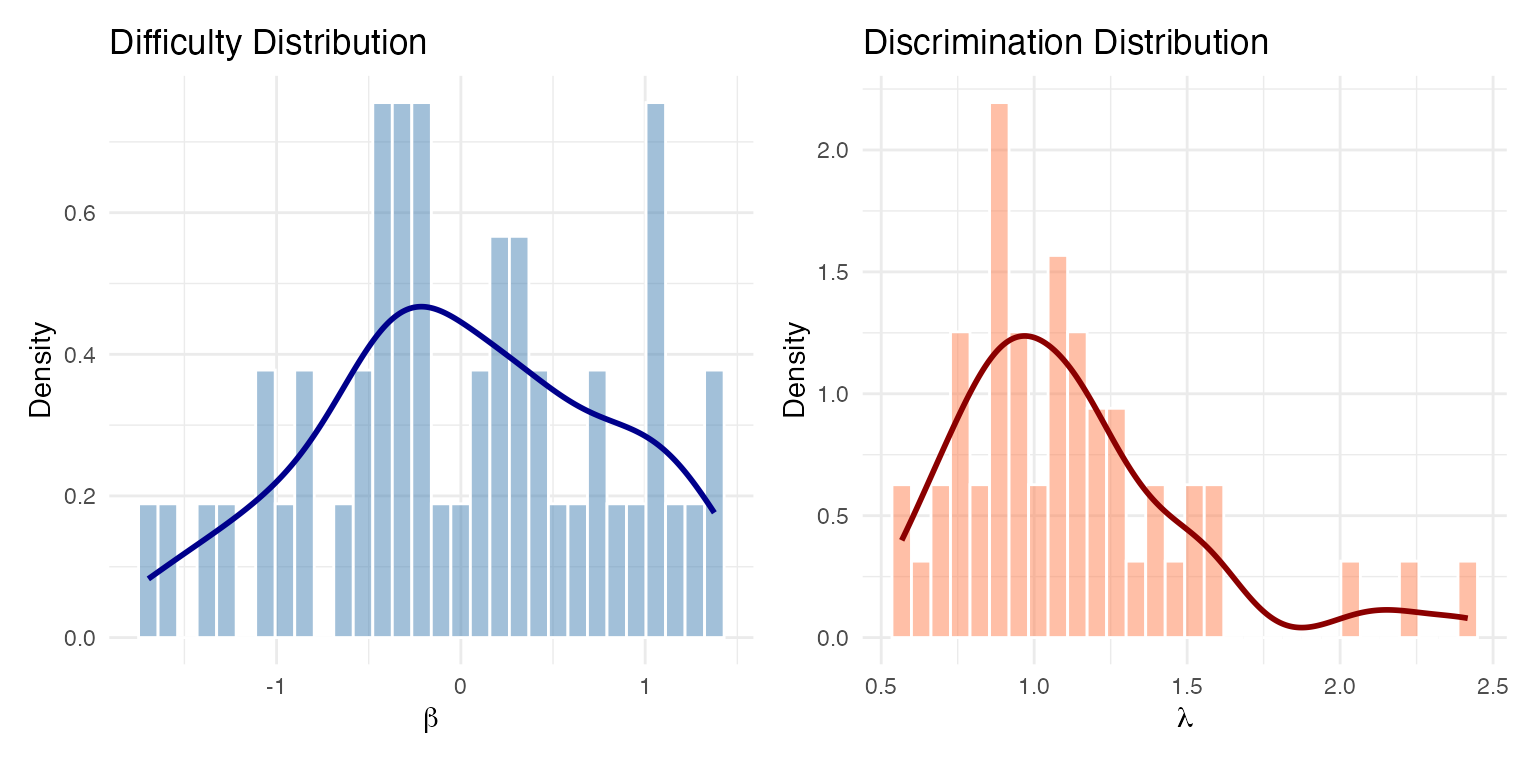

# Combined view (requires patchwork package)
plot(items_viz, type = "both")

Integration with eqc_calibrate

In the reliability-targeted simulation framework, sim_item_params() is called internally by eqc_calibrate(). You specify item generation settings through the item_source and item_params arguments:

# EQC automatically calls sim_item_params internally
eqc_result <- eqc_calibrate(
  target_rho = 0.80,
  n_items = 25,
  model = "2pl",
  latent_shape = "normal",
  item_source = "irw",
  item_params = list(
    discrimination_params = list(
      mu_log = 0,
      sigma_log = 0.3,
      rho = -0.3
    )
  ),
  seed = 42
)

# The calibrated items are accessible
print(eqc_result$items_calib)

Accessing Calibrated Items

After calibration, you can access both baseline and calibrated item parameters:

# Baseline items (scale = 1)
items_base <- eqc_result$items_base

# Calibrated items (scale = c*)
items_calib <- eqc_result$items_calib

# The calibration factor
c_star <- eqc_result$c_star

Working with the Output Object

The item_params object contains rich information:

items <- sim_item_params(n_items = 25, model = "2pl", source = "irw", seed = 42)

# Structure
names(items)
#>  [1] "data"     "model"    "source"   "method"   "n_items"  "n_forms" 
#>  [7] "scale"    "centered" "params"   "achieved"

# Extract as data frame
df <- as.data.frame(items)
head(df)
#>   form_id item_id         beta    lambda lambda_unscaled
#> 1       1       1 -0.390285351 1.0379855       1.0379855
#> 2       1       2 -0.204977951 0.9979810       0.9979810
#> 3       1       3  1.140526381 1.0008540       1.0008540
#> 4       1       4  0.002368838 0.7685377       0.7685377
#> 5       1       5 -1.484244154 1.2348209       1.2348209
#> 6       1       6  0.428803529 1.0618176       1.0618176

# Achieved statistics
items$achieved$overall
#> $n_total
#> [1] 25
#> 
#> $beta_mean
#> [1] -2.664535e-17
#> 
#> $beta_sd
#> [1] 0.7991656
#> 
#> $lambda_mean
#> [1] 1.025717
#> 
#> $lambda_sd
#> [1] 0.3127527
#> 
#> $cor_pearson_pooled
#> [1] -0.2009709
#> 
#> $cor_spearman_pooled
#> [1] -0.3484615

Comparison of Methods

Let’s compare the three discrimination generation methods:

set.seed(123)

methods <- c("copula", "conditional", "independent")
results <- list()

for (m in methods) {
  results[[m]] <- sim_item_params(
    n_items = 200,
    model = "2pl",
    source = "irw",
    method = m,
    discrimination_params = list(rho = -0.4),
    seed = 123
  )
}

# Compare achieved correlations
cat("Method Comparison (target rho = -0.4):\n")
#> Method Comparison (target rho = -0.4):
cat("======================================\n")
#> ======================================
for (m in methods) {
  cat(sprintf("%-12s: Pearson = %+.3f, Spearman = %+.3f\n",
              m,
              results[[m]]$achieved$overall$cor_pearson_pooled,
              results[[m]]$achieved$overall$cor_spearman_pooled))
}
#> copula      : Pearson = -0.526, Spearman = -0.527
#> conditional : Pearson = -0.495, Spearman = -0.466
#> independent : Pearson = -0.077, Spearman = -0.045

The copula method achieves the target Spearman correlation most reliably.

Summary Table: Sources and Methods

Source Description Best For
irw Item Response Warehouse Realistic simulations
parametric Normal/uniform difficulties Controlled experiments
hierarchical Joint MVN generation Bayesian framework
custom User-supplied parameters Specific scenarios
Method Preserves Marginals Target Correlation Notes
copula Yes Spearman Recommended
conditional No Pearson Assumes normality
independent Yes None (0) No correlation

Practical Recommendations

For Realistic Simulations 

items <- sim_item_params(
  n_items = 30,
  model = "2pl",
  source = "irw",           # Use IRW
  method = "copula",        # Preserve marginals
  discrimination_params = list(
    mu_log = 0,
    sigma_log = 0.3,
    rho = -0.3              # Empirical correlation
  ),
  seed = 42
)

For Controlled Experiments 

items <- sim_item_params(
  n_items = 25,
  model = "2pl",
  source = "parametric",
  difficulty_params = list(mu = 0, sigma = 1),
  method = "conditional",
  discrimination_params = list(
    mu_log = 0,
    sigma_log = 0.25,
    rho = 0                 # No correlation for clean design
  ),
  seed = 42
)

For Bayesian Frameworks 

items <- sim_item_params(
  n_items = 25,
  model = "2pl",
  source = "hierarchical",
  hierarchical_params = list(
    mu = c(0, 0),
    tau = c(0.3, 1),
    rho = -0.3
  ),
  seed = 42
)

References

Glas, C. A. W., & van der Linden, W. J. (2003). Computerized adaptive testing with item cloning. Applied Psychological Measurement, 27(4), 247-261.

Sweeney, S. M., et al. (2022). An investigation of the nature and consequence of the relationship between IRT difficulty and discrimination. Educational Measurement: Issues and Practice, 41(4), 50-67.

Zhang, L., Fellinghauer, C., Geerlings, H., & Sijtsma, K. (2025). Realistic simulation of item difficulties using the Item Response Warehouse. PsyArXiv. https://doi.org/10.31234/osf.io/r5mxv